- 重复组合

重复组合
基本介绍
定义
一般地,从![]() 个不同的元素中,每次取出
个不同的元素中,每次取出![]() 个可以重复的元素并成一组,叫做从
个可以重复的元素并成一组,叫做从![]() 个不同的元素每次取出
个不同的元素每次取出![]() 个元素的允许重复的组合,即重复组合,其组合总数记作
个元素的允许重复的组合,即重复组合,其组合总数记作![]() 。
。
相关结论
关于重复组合的计数方法有下面的规律。
定理1从![]() 个不同的元素每次取出
个不同的元素每次取出![]() 个元素的允许重复的组合总数为
个元素的允许重复的组合总数为
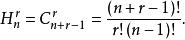
证法1:设有![]() 个不同的元素,不失一般性,可设为
个不同的元素,不失一般性,可设为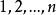 。
。
设从这![]() 个不同的元素取出
个不同的元素取出![]() 个元素的重复组合为
个元素的重复组合为
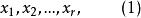 且假定
且假定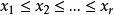 ,这里有等号出现是因为元素允许重复。
,这里有等号出现是因为元素允许重复。
我们再构造一个组合
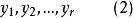 与组合(1)相对应,其对应关系是
与组合(1)相对应,其对应关系是
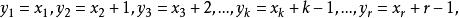 显然这种对应是一一对应。
显然这种对应是一一对应。
在这个对应中,虽然组合(1)中的元素有可能相同,但是组合(2)中的元素却都不相同,这样,组合(2)就是一个没有重复元素的组合。
组合(2)是从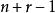 个不同的元素中,取出r个不同元素的组合,组合数为
个不同的元素中,取出r个不同元素的组合,组合数为![]() 。由于组合(2)的组合数与组合(1)的组合数相同,所以组合(1)的组合数为
。由于组合(2)的组合数与组合(1)的组合数相同,所以组合(1)的组合数为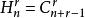 。
。
关于这个证明,我们给出一个直观的例子:
例如,从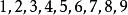 中取出5个允许重复的组合,其中一个组合是
中取出5个允许重复的组合,其中一个组合是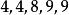 。
。
对于这个组合,采用证法中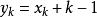 的构造方法,就是
的构造方法,就是
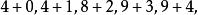 即
即
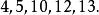 这第二个组合的元素没有重复,第二个组合相当于从
这第二个组合的元素没有重复,第二个组合相当于从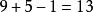 (个)元素中取出5个不同元素的组合。组合数为
(个)元素中取出5个不同元素的组合。组合数为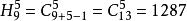 。
。
证法2:设有n个不同的元素,不失一般性,可设为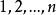 。
。
从![]() 个不同的元素取出r个元素的重复组合为
个不同的元素取出r个元素的重复组合为
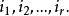
设元素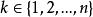 在组合中出现了
在组合中出现了![]() 次,其中
次,其中![]() 是非负整数,若
是非负整数,若![]() ,则说明元素k在组合中没有出现;若
,则说明元素k在组合中没有出现;若![]() ,则说明元素k在组合中出现2次;……
,则说明元素k在组合中出现2次;……
由此,一次不定方程
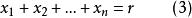 的任一组非负整数解就对应着一个
的任一组非负整数解就对应着一个![]() 个元素的重复组合。
个元素的重复组合。
所以,从![]() 个不同的元素取出
个不同的元素取出![]() 个元素的重复组合数,就是一次不定方程③的非负整数解的个数,其个数为
个元素的重复组合数,就是一次不定方程③的非负整数解的个数,其个数为![]() ,即
,即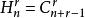 。
。
我们也给出一个例子来说明这个证法。
例如,从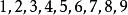 中取出5个允许重复的组合,其中一个组合是
中取出5个允许重复的组合,其中一个组合是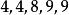 ,对应着一次不定方程
,对应着一次不定方程
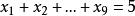 的一组解
的一组解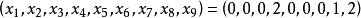 。
。
同样,组合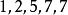 对应着解
对应着解
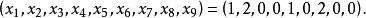 所以,求从
所以,求从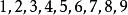 中取出5个允许重复的组合数的问题就转化为一次不定方程
中取出5个允许重复的组合数的问题就转化为一次不定方程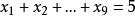 的非负整数解问题,即[2]
的非负整数解问题,即[2]
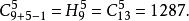
例题解析
例1邮局发行10种新邮票,有一个集邮爱好者购买了15张邮票,他有多少种买法?
解:买邮票的任何一种方式都可以看做是从10个元素中取出15个元素的组合,因此买法种数为
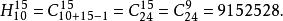
例2求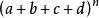 的展开式的项数。
的展开式的项数。
解:由于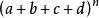 的展开式的每一项都是n次的,因此,展开式的每一项都是从
的展开式的每一项都是n次的,因此,展开式的每一项都是从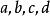 这4个元素中取出n个元素的重复组合,不同的组合就得到不同的项,所以,
这4个元素中取出n个元素的重复组合,不同的组合就得到不同的项,所以,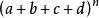 的展开式的项数为
的展开式的项数为
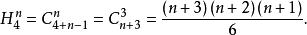
例3有一枚硬币,正面是国徽,反面是币值,我们同时投掷5枚这样的硬币,会出现多少种不同的情况呢?
把各种不同的情况一一列举出来就是:
| 正面 | 5 | 4 | 3 | 2 | 1 | 0 |
| 反面 | 0 | 1 | 2 | 3 | 4 | 5 |
如果我们把硬币的“正面”和“反面”看成两个不同的元素,那么这个问题就是:从两个不同的元素中,取出5个元素的组合,显然,所取的元素允许重复。
又如,从3个元素的集合![]() 中,取2个元素,如果允许所取得元素重复,则有
中,取2个元素,如果允许所取得元素重复,则有
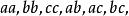 共6种[2]。
共6种[2]。

-
一汽奔腾B2 搭载1.5T+7DCT动力组合
2025-09-20 13:25:46 查看详情 -
一汽首款插混MPV 搭载1.5T+7DCT动力组合
2025-09-20 13:25:46 查看详情 -
一汽奔腾MPV车型谍照曝光 搭载1.5T+7DCT动力组合
2025-09-20 13:25:46 查看详情 -
一汽丰田bZ3正式发布 搭载1.5T+7DCT动力组合
2025-09-20 13:25:46 查看详情 -
铝制柱翼型组合式散热器
2025-09-20 13:25:46 查看详情 -
硬齿面无级行星组合变速机
2025-09-20 13:25:46 查看详情 -
10kV级组合式变压器
2025-09-20 13:25:46 查看详情


 求购
求购

