等边对等角

在同一三角形中,两条边相等,则两个边的对角相等,即等边对等角,如等腰直角三角形，是 等角对等边的逆定理（这是公理）

等边对等角的相关习题(5)1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。

2.等腰三角形的顶角平分线，底边上的中线，底边上的高相互重合（简写成“等腰三角形三线合一”）。

3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。

4.等腰三角形底边上的垂直平分线到两条腰的距离相等。

5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。

6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。

7.一般的等腰三角形是轴对称图形,只有一条对称轴，顶角平分线所在的直线是它的对称轴。但等边三角形（特殊的等腰三角形）有三条对称轴。每个角的角平分线所在的直线，三条中线所在的直线，和高所在的直线就是等边三角形的对称轴。

8.等腰三角形中腰长的平方等于底边上高的平方加底的一半的平方（勾股定理）。

等腰三角形的腰与它的高的关系：

直接的关系是：腰大于高。间接的关系是：腰的平方等于高的平方加底的一半的平方。^[1]

定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。

判定定理：在同一三角形中，如果两个角相等，那么这两个角所对的边也相等（简称：等角对等边）。

除了以上两种基本方法以外，还有如下判定的方式：

• 在一个三角形中，如果一个角的平分线与该角对边上的中线重合，那么这个三角形是等腰三角形，且该角为顶角。

• 在一个三角形中，如果一个角的平分线与该角对边上的高重合，那么这个三角形是等腰三角形，且该角为顶角。

• 在一个三角形中，如果一条边上的中线与该边上的高重合，那么这个三角形是等腰三角形，且该边为底边。

  显然，以上三条定理是“三线合一”的逆定理。

• 有两条角平分线（或中线，或高）相等的三角形是等腰三角形。

• 有两边相等且有一个角的度数是60度的三角形是等边三角形。

如图，在△ABC中，AB=AC，求证：∠B=∠C 。

证明：

作AD平分∠BAC

∴∠BAD=∠CAD( 角平分线定义）

在△ABD与△ACD中：

AB=AC（已知）

∠BAD=∠CAD（已证）

AD=AD（公共边）

∴△ABD≌△ACD（SAS）

∴∠B=∠C（ 全等三角形的 对应角相等）

证明：

作AD⊥BC于D

∴∠ADB=∠ADC=90度

∴在Rt△ABD与Rt△ACD中：

AB=AC(已知)

AD=AD（公共边）

∴Rt△ABD≌Rt△ACD（HL）

∴∠B=∠C（全等三角形的对应角相等）

证明：

作△ABC中线AD交BC于点D

∵AD是BC中线，

∴BD=CD

在△ABD与△ACD中：

AD=AD（公共边）

AC=AB（已知）

BD=CD（已知）

∴△ABD≌△ACD（SSS）

∴∠B=∠C（全等三角形的对应角相等）

证明：

在△ABC和△ACB中:

AB=AC(已知)

BC=CB(公共边)

AC=AB(已知)

∴△ABC≌△ACB(SSS)

∴∠B=∠C(全等三角形的对应角相等)

（正弦定理）

∵AB=AC，AB/sinC=AC/sinB

∴sinB=sinC

∴B=C或B+C=180°

∵AB交AC於A

∴B+C≠180°

∴B=C

（余弦定理）

cosB=(AB²+BC²-AC²)/(2*AB*BC)

cosC=(AC²+BC²-AB²)/(2*AC*BC)

∵AB=BC

∴两式相减，化简得cosB=cosC

∴B=C

等边对等角2ab<A<b+a

可见大三角形底边的邻近区域无法由小三角形不重叠又不超地来填充。故命题错。

另外一种黄金三角形是腰与底的比值为（√5-1)/2的等腰三角形，顶角为108°，底角为36°。

设小三角形的底为a，则腰为b=（√5-1)a/2。

同样可以证明：

A=2b+a

2b<B<3b

a<B<b+a

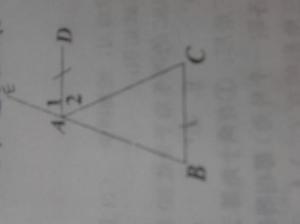
可见大三角形腰的邻近区域无法由小三角形不重叠又不超出地填充（图2）。故命题错。

事实上，勾为a，股为b=2a的直角三角形可以满足命题要求。

显然，弦c=√a2+b2 =√5 a。

三角形的对应边：

A=√5 a=c，

B=2A=2c，

C=√5 *（√5a)=5a=2b+a 。

满足上述必要条件。是否成立还要验证，结果是对的。本三角形是否唯一满足命题还不清楚。

顶角36°的黄金三角形按任意一底角的角平分线分成两个小等腰三角形，且其中一个等腰三角形的底角是另一个的2倍。顶角是108°的黄金三角形把顶角一个72°和一个36°的角，这条分线也把黄金三角形分成两个小等腰三角形，且其中一个等腰三角形的底角也是另一个的2倍。

①AB=AC，AD⊥BC，

∴AD平分∠BAC(或BD=CD)；

②∵AB＝AC，BD＝DC，

∴AD⊥BC(或AD平分∠BAC)；

③∵AB＝AC，AD平分∠BAC，

∴BD＝DC(或AD⊥BC)。

等边对等角的悖论

命题：如果有一个三角形，那么该三角形为等腰三角形。

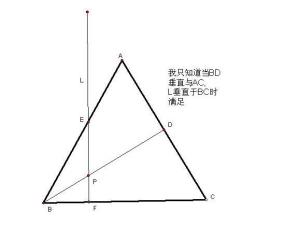
论证：在△ABC中，E是∠A的角平分线和BC垂直平分线的交点，EF，EG是垂直于边AB，AC的垂足是F，G．容易得到△AEF≌△AEG(ASA)，△EFB≌△EGC(HL)．所以有AF=AG，BF=CG，所以有AB=AC，三角形ABC是等腰三角形了！

这个结论肯定是错误的，因为很容易作出一个三条边长分别为3，4，5的三角形，利用反证法即可推翻该悖论，它当然不是等腰三角形，而我们的结论却说这样一个三角形也一定是等腰的。那么，错误出在哪里呢？

问题在于：E点的位置一般来说总在△ABC的外面（且在非等腰三角形中得到的两条线段一个是加一个减，必定不相等）而不是它的里面。可见正确作图也可以帮助我们理解许多问题。

说明：在△ABC中，D是∠A的角平分线和BC垂直平分线的交点,由图可知，无论是锐角、直角还是钝角三角形，点D都不在△ABC内。

现在，这条悖论就不攻自破了。