反演定理

反演定理是这样表述的：对于任意一个逻辑式，如果把其中所有的“”换成“+”，“+”换成“”，0换成1，1换成0，原变量换成反变量，反变量换成原变量，得到的结果就是。^[1]

在运用反演定理时还需注意遵守以下规则：

(1)仍需遵守“先括号内，后括号外，先乘后加”的运算顺序；

(2)不属于单个变量上的反号应保留不变。

用反演定理可以很方便地求出逻辑函数的反函数。^[1]

例1已知逻辑函数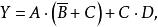求。

解：根据反演定理可写出：

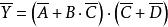
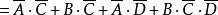
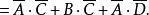
例2已知逻辑函数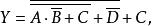求。

解：根据反演定理可写出：

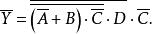
例3求函数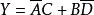的反函数。

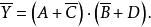解：

例4求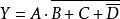函数的反函数。

解：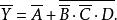

注意：

(1)要注意运算的优先顺序(先括号，然后乘，最后加)，必要时加括号，如例3。

(2)变换中，几个变量(一个以上)的公共非号保持不变，如例4。^[2]