- 块三对角矩阵
块三对角矩阵
简介
在线性代数中,块三对角矩阵是矩阵的一种,它“几乎”是一个对角矩阵。准确来说:一个块三对角矩阵的非零系数在如下的三条对角线上:主对角线、低对角线、高对角线。在许多物理问题中,块三对角矩阵常常作为原始数据出现,因此它们本身是很重要的,这种矩阵仅有(2n-1)个独立的元素。由块三对角矩阵确定特征值由一些较有效的方法,常见的有两种:QR法、特征多项式法。
定义
形如
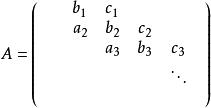
的n×n矩阵A称为块三对角矩阵,其中第(i,j)个元素在j>i+1和j<i-1时为零。
块三对角矩阵的特点
块三对角矩阵M是一个对角矩阵,当且仅当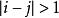 时,有M(i,j)=0。在一个nxn的块三对角矩阵T中,非0元素排列在如下的三条对角线上:
时,有M(i,j)=0。在一个nxn的块三对角矩阵T中,非0元素排列在如下的三条对角线上:
(1)主对角线即i=j;
(2)主对角线之下的对角线(称低对角线)即i=j+1;
(3)主对角线之上的对角线(称高对角线)即i=j-1。
这块三条对角线上的元素总数为3n-2,故可以使用一个拥有3n-2个位置的一维数组来描述T,因为仅需要存储块三条对角线上的元素。
确定块三对角矩阵的特征值
QR法
QR法对于三对角矩阵来说是很好的,在这个方法中,矩阵被分解成以下形式: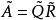 ,其中
,其中![]() 是正交矩阵,
是正交矩阵,![]() 是上三角矩阵。产生如下的矩阵序列:将
是上三角矩阵。产生如下的矩阵序列:将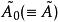 化成乘积形式
化成乘积形式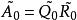 ,则
,则![]() 定义为
定义为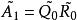 。
。
一般来说,对于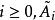 化成
化成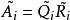 ,其中
,其中![]() 是正交矩阵,
是正交矩阵,![]() 是上三角矩阵,则
是上三角矩阵,则![]() 被定义为
被定义为![]() 和
和![]() 以相反次序乘积式。因为
以相反次序乘积式。因为![]() 是正交矩阵,
是正交矩阵,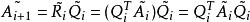 。
。![]() 是对称的,与
是对称的,与![]() 有相同的特征值。我们定义
有相同的特征值。我们定义![]() 和
和![]() 成这样的形式:
成这样的形式:![]() 是块三对角矩阵,最终
是块三对角矩阵,最终![]() 趋于变为对角阵,其对角线上的元素给出原矩阵的特征值。
趋于变为对角阵,其对角线上的元素给出原矩阵的特征值。
特征多项式法
特征多项式法可以像特征多项式![]() 的根一样确定特征值。有一种有效的方法来构造块三对角矩阵的特征多项式。使用符号法可以求特征值的归类,从而形成一个Sturmian序列。然后用对分法或试位法来求精确的特征值。由Householder变换得到的对称块三对角矩阵的特征多项式为:
的根一样确定特征值。有一种有效的方法来构造块三对角矩阵的特征多项式。使用符号法可以求特征值的归类,从而形成一个Sturmian序列。然后用对分法或试位法来求精确的特征值。由Householder变换得到的对称块三对角矩阵的特征多项式为:
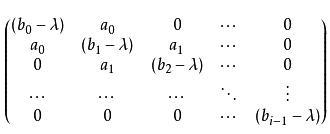
其中,i=1,2,...,n,有:
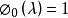
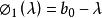
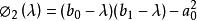
从![]() 向前的Sturm序列可以表示为:
向前的Sturm序列可以表示为:
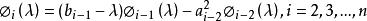
因此有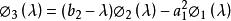



 求购
求购










