- 对偶定理

对偶定理
定义
对偶定理是揭示原始问题的解与对偶问题的解之间重要关系的一系列定理。
(对偶定理) 设Y,y,γ以及S,s同前,如果存在可容许的向量p和ξ,则S和s都有限,并且S=s[2].
举例
若Y=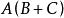 ,则Y'=
,则Y'=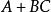 ;
;
若Y=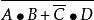 ,则Y'=
,则Y'=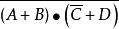 ;
;
若Y=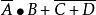 ,则Y'=
,则Y'=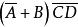 .
.
若两逻辑式相等,则它们的对偶式也相等,这就是对偶定理(Duality theorem)。
同一个电路,按正逻辑和负逻辑规定所得到的逻辑表达式不一定相等,也不一定相反,它们之间是对偶的关系。所以如果两个电路在正逻辑下是相等的,那么在负逻辑下也必定是相等的,这就是对偶定理的实质[3]。
有时候直接证明两个逻辑式相等比较麻烦,但其对偶式的证明比较简单,可以先证明其对偶式相等,再利用对偶定理就得到原式相等[1]。
性质定理与推论
性质对偶问题的对偶仍是原问题。
定理1(弱对偶定理)如果![]() 是原问题的可行解,
是原问题的可行解,![]() 是对偶问题的可行解,则恒有[1]
是对偶问题的可行解,则恒有[1]
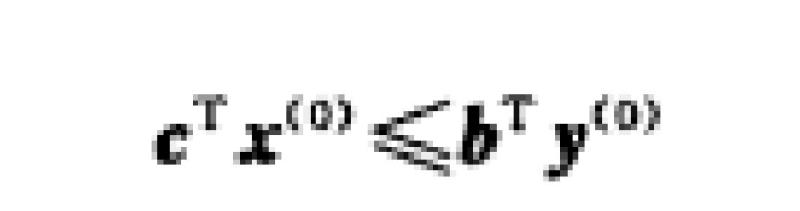
推论1原问题任一可行解的目标函数值是其对偶问题目标函数值的下界;反之对偶问题任一可行解的目标函数值是其原问题目标函数值的上界。[4]
定理2(最优准则定理) 如果![]() 是原问题的可行解,
是原问题的可行解,![]() 是对偶问题的可行解,则当
是对偶问题的可行解,则当![]()
![]() =
=![]()
![]() 时,
时,![]() 、
、![]() 分别为各自问题的最优解。
分别为各自问题的最优解。
定理3(最优解存在定理) 若原问题和对偶问题同时存在可行解,则它们必都存在最优解。
证明:最大化问题LP的目标函数值有上界,所以一定有最优解,类似地,最小化问题
DP的目标函数值有下界,所以也一定有最优解。
证毕。
定理4(无界解定理) 若原问题(或对偶问题)有可行解且目标函数值无界,则其对偶问题(或原问题)无可行解。
定理5(强对偶性定理) 如果原问题和对偶问题中有一个有最优解,则另一个问题也必存在最优解,且两个问题的最优解的目标函数值相等。[1]
推论2设![]() ,
,![]() 分别是对称形式的原问题式和其对偶问题式的可行解,则
分别是对称形式的原问题式和其对偶问题式的可行解,则![]() ,
,![]() 分别是原问题和对偶问题的最优解的充分必要条件为
分别是原问题和对偶问题的最优解的充分必要条件为![]()
![]() =
=![]()
![]() .
.
推论3若原问题式有最优解,则在其最优单纯形表中,松弛变量的检验数的负值即为对偶问题的一个最优解。
定理6(互补松弛性定理) (向量形式)设x,y分别是对称形式的原问题式和其对偶问题式的可行解,则x,y分别是原问题和对偶问题的最优解的充分必要条件为:
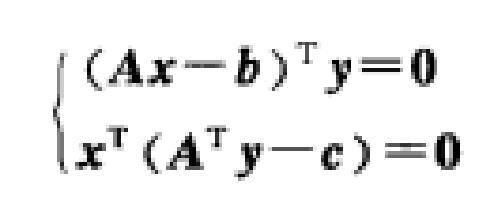
(分量形式)设x=(x1,x2,…,xn)T,y=(y1,y2,…,yn)T分别是原问题式和其对偶问题式的可行解,则x,y分别是原问题和对偶问题的最优解的充分必要条件为:[4]
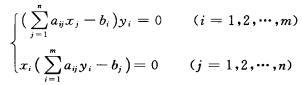



 求购
求购







