- 三面角

三面角
1定义编辑
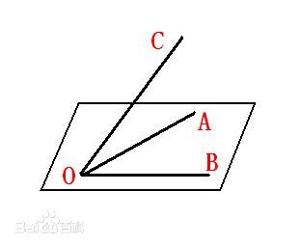
三面角:由三个面构成的多面角称为三面角,如图中三
面角可记作∠O-ABC。特别地,三个面角都是直角的三面角称为直三面角。
 三面角的补三面角:由三条自已知三面角定点发出的垂直于已知三面角的三个平面的射线组成的三面角叫做已知三面角的补三面角。
三面角的补三面角:由三条自已知三面角定点发出的垂直于已知三面角的三个平面的射线组成的三面角叫做已知三面角的补三面角。
2性质编辑
1、三面角的任意两个面角的和大于第三个面角。
2、三面角的三个二面角的和大于180°,小于540°。
3三面角相关定理编辑
设三面角∠O-ABC的三个面角∠AOB、∠BOC、∠AOC所对的二面角依次为∠OC,∠OA,∠OB。
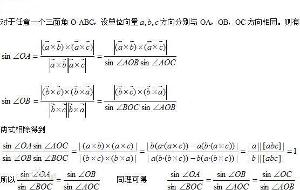
1、三面角正弦定理:
sin∠OA/sin∠BOC=sin∠OB/sin∠AOC=sin∠OC/sin∠AOB。
证明过程如下:
2、三面角第一余弦定理:
cos∠BOC=cos∠OA×sin∠AOB×sin∠AOC+cos∠AOB×cos∠AOC。
证明过程如下:
三面角余弦定理证明
3、三面角第二余弦定理:cos∠OA=cos∠BOC×sin∠OB×sin∠OC-cos∠OB×cos∠OC。
从三面角第一余弦定理中消去∠AOB和∠AOC即可得


相关百科


 求购
求购








