多面角

多面角是立体几何研究的基本图形。

由若干条具有公共端点且不共面的有序射线 SA,SB,SC,...,SL 以及相邻设射线所组成的角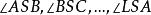（约定都小于平角）的内部构成的立体图形称为多面角，记为 S-AB...L。

公共端点称为多面角的顶点，射线 SA,SB,SC,...,SL 称为多面角的棱，相邻两棱所夹的角称为多面角的面角，相邻两棱间的平面部分称为多面角的面，不相邻的棱间的平面部分称为多面角的对焦面，相邻两个面所成的二面角称为多面角的二面角，亦称多面角的棱角。

若多面角有 n 个面，就称它是 n 面角。n 面角有 n 条棱，n 个面和 n 个二面角。^[1]

(acute polyhedral angle)锐多面角是一种特殊的多面角，指以多面角的顶点为球心作单位球面，如果多面角在单位球面上截出的部分（球面多边形）的面积小于全球面面积的八分之一，则称该多面角为锐多面角。

平面内的一条直线，把这个平面分为两部分，每一部分都叫作半平面。从一条直线出发的两个半平面所组成的图形叫作二面角。这条直线叫作二面角的棱，这两个半平面叫作二面角的面。二面角的大小，可以用它的平面角来度量，二面角的平面角是几度，就说这个二面角是几度。二面角也可以看作是从一条直线出发的一个半平面绕着这条直线旋转，它的最初位置和最终位置组成的图形。