- 半正多面体

半正多面体
中文名
半正多面体
所属学科
数学
别称
阿基米德体、阿基米德多面体
基本介绍
多面体的多面角都合同,当这些多面角由两种(及)以上正多边形构成,则多面体称为半正多面体。例如把正四面体一条棱各三等分,沿三等分点从原体割去四个小正四面体,余下的多面体就成为半正多面体,它的多面角都合同,这些多面角都由1个正三角形,2个正六边形构成。这一半正多面体我们记为3·62。
阿基米德发现了全部13个可能的所谓半正多面体。正多面体的面都是同一类型的正多边形,而半正多面体是一个凸多面体,它的面也是正多边形,但并非全都是同一种类型。例如,如果我们从一个立方体a的8个角上各切掉一个边长为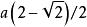 的四面体,结果得到的图形就是一个半正多面体,或称阿基米德多面体,其表面由8个等边三角形和6个正八边形构成[2]。
的四面体,结果得到的图形就是一个半正多面体,或称阿基米德多面体,其表面由8个等边三角形和6个正八边形构成[2]。
半正多面体有13种
命题半正多面体(表1)有13种:
![]()
![]()
![]()
![]() 我们用
我们用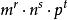 表示每一多面角由r个正m边形,s个正n边形,t个正p边形构成的半正多面体[3]。
表示每一多面角由r个正m边形,s个正n边形,t个正p边形构成的半正多面体[3]。
| 种类 | 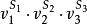 |
面数F | 顶点数V | 棱数E | 体积为1的棱长 |
| 3·62 | 8 | 12 | 18 | 0.717 | |
| 3·4·3·4 | 14 | 12 | 24 | 0.445 | |
| 4·62 | 14 | 24 | 36 | 0.263 | |
| 3·82 | 14 | 24 | 36 | 0.419 | |
| 3·5·3·5 | 32 | 30 | 60 | 0.227 | |
| 5·62 | 32 | 60 | 90 | 0.486 | |
| 3·43 | 26 | 24 | 48 | 0.751 | |
| 34·4 | 38 | 24 | 60 | 0.417 | |
| 3·102 | 32 | 60 | 90 | 0.287 | |
| 3·4·5·4 | 62 | 60 | 120 | 0.502 | |
| 4·6·8 | 26 | 48 | 72 | 0.296 | |
| 34·5 | 92 | 60 | 150 | 0.288 | |
| 4·6·10 | 62 | 120 | 180 | 0.169 |
命题半正多面体只有13种。
证明我们记每一多面角顶点围绕s个正多边形,其中s₁个正r₁边形,s₂个正r₂边形,......sn个正rn边形,s=s1+s2+...+sn,又设此半正多面体中共有![]() 个正r₁边形,
个正r₁边形,![]() 个正r₂边形,....,
个正r₂边形,....,![]() 个正rn边形,则
个正rn边形,则
![]() 而
而
![]() 又
又
![]() 把(i)~ (iii)代人Euler示性数公式v+f=e+2,并进行整理,得到半正多面体的特征方程[3]:
把(i)~ (iii)代人Euler示性数公式v+f=e+2,并进行整理,得到半正多面体的特征方程[3]:
![]()
半正多面体的性质
| 种类 | 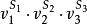 |
面数F | 顶点数V | 棱数E | 体积为1的棱长 |
| 3·62 | 8 | 12 | 18 | 0.717 | |
| 3·4·3·4 | 14 | 12 | 24 | 0.445 | |
| 4·62 | 14 | 24 | 36 | 0.263 | |
| 3·82 | 14 | 24 | 36 | 0.419 | |
| 3·5·3·5 | 32 | 30 | 60 | 0.227 | |
| 5·62 | 32 | 60 | 90 | 0.486 | |
| 3·43 | 26 | 24 | 48 | 0.751 | |
| 34·4 | 38 | 24 | 60 | 0.417 | |
| 3·102 | 32 | 60 | 90 | 0.287 | |
| 3·4·5·4 | 62 | 60 | 120 | 0.502 | |
| 4·6·8 | 26 | 48 | 72 | 0.296 | |
| 34·5 | 92 | 60 | 150 | 0.288 | |
| 4·6·10 | 62 | 120 | 180 | 0.169 |

相关百科


 求购
求购









