- 垂心四面体

垂心四面体
定义
垂心四面体(orthocentric tetrahedron)一种特殊的四面体。有两双对棱互相垂直的四面体,称为垂心四面体或正交四面体。垂心四面体的四条高线必相交于一点,这点称为垂心四面体的垂心。垂心四面体的一个特例是有一个三面角是三直三面角的四面体,称为三直角四面体。它的垂心就是三直三面角的顶点。正四面体也是垂心四面体的特例,它的垂心就是正四面体的重心。只有垂心四面体才有垂心一般的四面体未必存在垂心。
在几何学中,正中心的四面体是四面体,所有三对相对的边都是垂直的。它也被称为正交四面体,因为正交意味着垂直。1782年,Simon Lhuilier首先研究了它,并于1890年得到了G. de Longchamps的正中心四面体。
在一个正中心的四面体中,四个高度是并发的。这个共同点就是所谓的垂心,它有它是中心的对称点属性外接球关于心。因此,正中心与四面体的Monge点重合。
表征
所有的四面体都可以刻成平行六面体。四面体是正中心的,当且仅当它的外接平行六面体是菱面体。事实上,在任何四面体中,当且仅当外接平行六面体的相应面是菱形时,一对相对的边才是垂直的。如果一个平行六面体的四个面是菱形的,那么所有的边都是相同的长度,六个面都是菱形的;因此,如果四面体中的两对相对的边是垂直的,那么第三对是相同的,而四面体是正中心的。
一个四面体ABCD是正中心的,当且仅当相反边的平方和等于三对相对边时:
![]()
实际上,只有两对相对边满足四面体正中心的条件就足够了。
另外一个四面体正中心的充要条件是它的三个双生子具有相同的长度。
音量
关于边缘的表征意味着如果只有正中心四面体的六个边中的四个是已知的,则剩下的两个边可以被计算,只要它们彼此不相反即可。因此,正中心四面体的体积可以用四个边a,b,c,d表示。公式是
![]()
其中Ç和d是相对的边缘,并且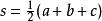 。
。
垂心四面体性质
1、 一组对棱垂直的四面体,过这组对棱中任一 条的两端点所作的两高线必相交。
2、若四面体从两顶点所作两条高线相交,则过此两顶点的棱垂直其对棱 。
3、 各面是菱形的平行六面体,其内接四面体是垂心四面体。
4、 任一顶点在对面的射影是对面 三角形垂心的四面体是垂心四 面体。
5、对棱中点连线相等的四面体呈垂心四面体。
6、 平行于四面体任一组对棱的平面截,其余四条棱若截口为矩形,则此四 面体为垂心四 面体。
7、 对棱平方和相等的四面体为垂心四面体。
8、 六棱中点在同一球面上的四面体是垂心四 面体。

-
我的爱从四面八方攻击你
2025-11-01 09:03:42 查看详情


 求购
求购









