圆内接六边形

内接于圆的正六边形是圆内接正六边形。

1、圆内接正六边形每条边长度相等（即圆的六条弦长度相等），且等于内接圆的半径；

2、圆内接正六边形的六个内角相等，都是120°；

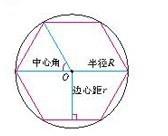圆内接正六边形的半径，中心角与边心距3、圆内接正六边形的每条边在圆内所对的优弧长度相等；

4、圆内接正六边形的每条边在圆内所对的优弧的弧度数相等；

5、圆内接正六边形的每条边在圆内所对的劣弧长度相等；

6、圆内接正六边形的每条边在圆内所对的劣弧的弧度数相等；

7、圆内接正六边形的每条边在圆内所对的圆心角（即每条边的中心角）相等，都是60°；

8、圆内接正六边形的边心距等于半径的（√3）/2倍。

1、圆内接正六边形的每条边在圆内所对的圆心角（即每条边的中心角）相等，都是60°。

在内接正六边形ABCDEF中

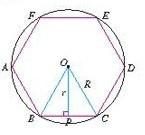图1 证明用图∵AB=BC=CD=DE=EF=FA

∴∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠FOA=360°÷6=60°

2、圆内接正六边形的边心距等于半径的√3/2倍。

如右图1

在正六边形ABCDEF中，BO=CO=BC

∴三角形BOC为等边三角形

∴∠OBC=60°

作OP⊥BC，垂足为P

在RT△OPB中

OP=r·sin60°=r√3/2

即圆内接正六边形的边心距等于半径的√3/2倍。