等面四面体

四个面相等的四面体称为等面四面体。三组对棱的长分别为a，b，c的等面四面体的体积计算公式为

式中u²=(a²+b²+c²)/2，表面积计算公式为

式中p=(a+b+c)/2，高h=12V/S=内切球半径r的4倍，外接球半径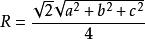，四个面的面积(或周长)皆相等的四面体是等面四面体。内切球与外接球同心的四面体必为等面四面体^[1]。

定理1一个四面体是等面四面体的充要条件是该四面体的外接平行六面体是长方体^[2]。

证明 充分性

设四面体ABCD的外接平行六而体AC₁BD₁-A₁CB₁D是长方体，那么AB=C₁D₁，CD=A₁B₁，因为AB=A₁B₁，所以AB=CD。同理可得AC=BD， AD= BC，所以四面体ABCD是等面四面体^[2]。

必要性

设平行六面体AC₁BD₁-A₁CB₁D是四面体ABCD的外接平行六面体，因为AB=CD，AB=C₁D₁，CD=A₁B₁，AB=A₁B₁，CD=C₁D₁，所以AB=C₁D₁，CD=A₁B₁，即平行四边形AC₁BD₁和平行四边形A₁CB₁D都是矩形，同理可得平行四边形AC₁CA₁和平行四边形B₁DD₁B都是矩形，平行四边形AA₁DD₁和平行四边形C₁CB₁B都是矩形，所以平行六面体AC₁BD₁-A₁CB₁D是长方体。

定理2一个四面体是等面四面体的充要条件是三双对棱中点的连线两两互相垂直。

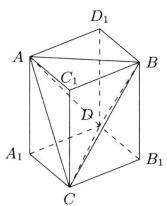图1

证明如图1，平行六面体AC₁BD₁-A₁CB₁D是四面体ABCD的外接平行六面体，则棱AB与CD中点的连线与AA₁平行，AC与BD的中点连线与AD₁平行，AD与BC的连线与AC₁平行。

充分性

当四面体ABCD三双对棱中点的连线两两互相垂直时，AA₁、AC₁、AD₁两两互相垂直，平行六面体AC₁BD₁-A₁CB₁D是长方体，由定理1知四面体ABCD是等面四面体^[2]。

必要性

如果四面体ABCD是等面四面体，那么AA₁、AC₁、AD₁两两互相垂直，所以四面体ABCD三双对棱中点的连线两两互相垂直。

定理3一个四面体是等面四面体的充要条件是对棱中点的连线是这双对棱的公垂线。

证明 如图1，平行六面体AC₁BD₁-A₁CB₁D是四面体ABCD的外接平行六面体，则棱AB与CD中点的连线与AA₁平行，AC与BD的中点连线与AD₁平行，AD与BC的连线与AC₁平行。

充分性

因为四面体ABCD对棱AB与CD中点的连线是AB与CD的公垂线，所以AA₁⊥平面AC₁BD₁，于是AA₁⊥AC₁,AA₁⊥AD₁.同理可得AC₁⊥AA₁,AC⊥AD₁,AD₁⊥AA₁，AD₁⊥AC₁，所以平行六面体AC₁BD₁-A₁CB₁D是长方体，由定理1知四面体ABCD是等面四面体。

必要性

因为四面体ABCD是等面四面体，所以平行六面体AC₁BD₁-A₁CB₁D是长方体，所以AB与CD的中点连线与平面AC₁BD₁、A₁CB₁D都垂直，即AB与CD的中点连线与AB、CD都垂直，所以AB与CD的中点连线是AB、CD的公垂线，同理可得AC与BD的中点连线是AC、BD的公垂线，AD与BC的中点连线是AD、BC的公垂线。

定理4一个四面体是等面四面体的充要条件是四面体四个面的周长都相等。

证明充分性

设四面体ABCD中AB=a, AC=b，AD=c，CD=p，BD=q，BC=r，且

a+b+r=a+b+q=b+c+ρ=p+q+r，

由a+b+r=p+q+r，a+c+q=p+q+r, 两边相加化简，得

2a+b+c=2p+q+r，

再由b+c+p=p+q+r得

b+c=q+ r，

所以a=p，同理得b=q，c=r，所以四面体ABCD是等面四面体^[2]。

必要性

如果四面体ABCD是等面四面体，那么AB=CD，AC=BD，AD=BC，所以△ABC≌△BAD≌△CDA≌△DCB，于是四面体ABCD的各面周长相等。

定理5一个四面体是等面四面体的充要条件是四面体四个面的面积都相等。

证明 充分性

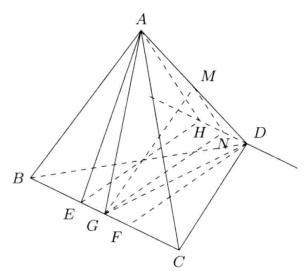图2

如图2，作四面体ABCD中△ABC和△BCD边BC的高AE和DF，点G是EF的中点，连AG、DG，过点D作l// BC，作EH⊥BC，与l相交于点H，连AH，点M是AD的中点，点N是DH的中点，连GN、MN，因为S△ABC= S△BCD，所以AB= DE。因为G是EF的中点，所以△AEG≌△DFG，因此AG= DG。因为点M是AD的中点，所以GM⊥AD.点G是EF的中点，点M是AD的中点，点N是DH的中点，MN//AH,GN//EH.因为AE⊥BC，EH⊥BC，所以BC⊥平面AEH，因此AH⊥BC，由此得MN⊥BC,GN⊥BC,所以BC⊥平面GMN,因此GM⊥BC,由此得GM是AD与BC的公垂线，并且经过AD的中点，同理可得AD与BC的公垂线经过BC的中点，即AD与BC的中点连线是AD、BC的公垂线，同理可得AB与CD的中点连线是AB、CD的公垂线，AC与BD的中点连线是AC、BD的公垂线，由定理3知四面体ABCD是等面四面体^[2]。

必要性

如果四面体ABCD是等面四面体，那么AB= CD，AC= BD，AD = BC，所以△ABC≌△BAD≌△CDA≌△DCB，于是S△ABC= S△BCD= S△ABD= S△ACD。

推论一个四面体是等面四面体的充要条件是该四面体的高都相等。

定理6一个四面体是等面四面体的充要条件是四面体内( 包括四面体各面所包含的三角形内的点以及棱上的点)任一点到该四面体各面距离的和是定值。

定理7一个四面体是等面四面体的充要条件是该四面体三双对棱为棱的二面角对应相等。

证明 充分性

设四面体ABCD中以AB、CD为棱的二面角相等，以AC、BD为棱的二面角相等，以AD、BC为棱的二面角相等，那么由三面角全等的判定定理知∠ABC=∠BAD，∠BAC=∠ABD，所以△ABC≌△BAD，于是AC=BD，AD=BC，同理可得AB=CD, 所以四面体ABCD是等面四面体^[2]。

必要性

因为四面体ABCD是等面四面体，那么∠BAC=∠BDC，∠BAD=∠ADC，∠CAD=∠ADB，由三面角全等的判定定理知四面体ABCD中以AB、CD为棱的二面角相等，同理可得四面体ABCD中以AC、BD为棱的二面角相等， 以AD、BC为棱的二面角相等。

定理8一个四面体是等面四面体的充要条件是该四面体每一顶点的三个面角的和都等于180°。

定理9一个四面体是等面四面体的充要条件是该四面体的每一顶点与对面三角形重心的连线等长。

定理10一个四面体是等面四面体的充要条件是从四面体任一顶点出发的三个面之间所成的三个二面角的余弦之和等于1^[2]。

定理11一个四面体是等面四面体的充要条件是四面体任一面与其他的面所成的三个二面角的余弦之和都等于1。

定理12等面四面体各面是全等的锐角三角形^[2]。

证明设四面体ABCD是等面四面体，所以AB= CD，AC= BD， AD=BC，因此△ABC≌△BAD≌△CDA≌△DCB，根据三面角的基本性质，得∠BAD+∠CAD>∠BAC，由定理8得∠BAC+∠BAD+∠CAD= 180°， 所以∠BAC< 90°。同理可得∠ABC < 90°，∠ACB < 90°，所以△ABC是锐角三角形。因为△ABC≌△BAD≌△CDA≌△DCB所以四面体ABCD各面是全等的锐角三角形。

定理13等面四面体的重心、外心、内心重合。

推论一个四面体是等面四面体的充要条件是该四面体的重心、外心、内心重合^[2]。