- 梯形中位线

梯形中位线
性质
 梯形中位线 梯形的中位线平行于两底,并且等于两底和的一半。
梯形中位线 梯形的中位线平行于两底,并且等于两底和的一半。
相关公式
 梯形中位线 面积公式:梯形中位线×高=(上底+下底)×高÷2=梯形面积
梯形中位线 面积公式:梯形中位线×高=(上底+下底)×高÷2=梯形面积
梯形中位线到上下底的距离相等
中位线长度=(上底+下底)÷2
相关比较
与三角形中位线作对比
|
三角形 |
梯形 |
中位线概念 |
连结三角形两边中点的线段叫做三角形的中位线. |
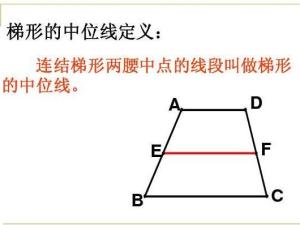
连结梯形两腰中点的线段叫做梯形的中位线。 |
要点 |
连结三角形两边中点的线段而不是连结一顶点和它的对边中点的线段 |
连结两腰中点的线段而不是连结两底中点的线段。 |
联系 |
三角形可看成上底为零的梯形。 |
|
中位线定理 |
三角形的中位线平行于第三边并且等于它的一半 |
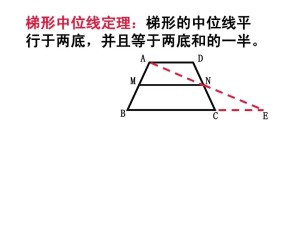
梯形的中位线平行于两底,并且等于两底和的一半。 |
定理证明
|
三角形 |
梯形 |
中位线概念 |
连结三角形两边中点的线段叫做三角形的中位线. |
连结梯形两腰中点的线段叫做梯形的中位线。 |
要点 |
连结三角形两边中点的线段而不是连结一顶点和它的对边中点的线段 |
连结两腰中点的线段而不是连结两底中点的线段。 |
联系 |
三角形可看成上底为零的梯形。 |
|
中位线定理 |
三角形的中位线平行于第三边并且等于它的一半 |
梯形的中位线平行于两底,并且等于两底和的一半。 |
相关误区
 梯形中位线如图1 梯形ABCD,E为AB的中点,F为CD的中点,连接EF,
梯形中位线如图1 梯形ABCD,E为AB的中点,F为CD的中点,连接EF,
求证:EF平行两底且等于两底和的一半。 证明:连结AF,并延长AF于BC延长线交于点O
在△ADF和△FCO中
∵ AD//BC
∴ ∠D=∠1 图1
又∵ ∠2=∠3 DF=CF
∴ △ADF≌△FCO
∵ 点E,F分别是AB,AO中点
∴ EF为三角形ABO中位线
∴ EF∥OB即EF∥BC
∵ AD//BC
∴ EF∥BC∥AD(EF平行两底)
∵ EF为三角形ABO的中位线
∴ 2EF=OB
OB=BC+CO CO=AD
∴ 2EF=BC+AD
∴ EF=(BC+AD)÷2(EF等于两底和的一半)
梯形的中位线平行于上下两底且等于两底和的一半
词条图册
 梯形中位线(3)
梯形中位线(3)
梯形的中位线是连结两腰中点的线段而不是连结两底中点的线段。
三角形中位线有三条,而梯形中位线只有1条。



 求购
求购








