中位线定理

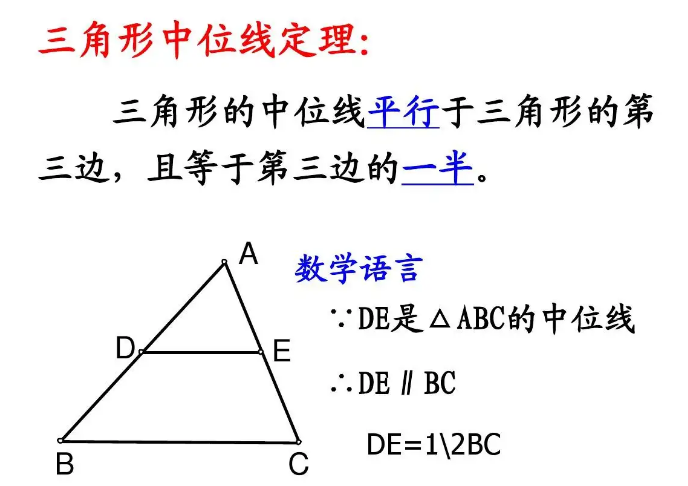中位线定理(3)（1）三角形中位线定义：连接三角形两边中点的线段叫做三角形的中位线。

（2）梯形中位线定义：连接梯形两腰中点的线段叫做梯形的中位线。^[2]

（1）要把三角形的中位线与三角形的中线区分开。三角形中线是连接一顶点和它的对边中点的线段，而三角形中位线是连接三角形两边中点的线段。

（2）梯形的中位线是连接两腰中点的线段而不是连结两底中点的线段。

（3）两个中位线定义间的联系：可以把三角形看成是上底为零时的梯形，这时三角形的中位线就变成梯形的中位线。

（1）三角形中位线定理：三角形的中位线平行于第三边并且等于它的一半．

（2）梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半．

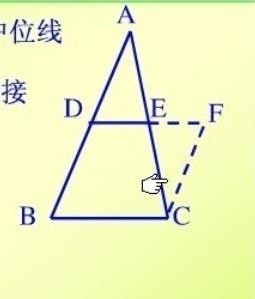中位线定理证明已知：如图，DE是△ABC的中位线

求证：DE∥BC DE=1/2 BC

证明：延长DE至F，使EF=DE，连接CF

∵DE是△ABC的中位线

∴AE=CE

在△ADE和△CFE中

∵AE=CE（已证），∠AED=∠CEF（对顶角相等），DE=EF（已作）

∴△ADE≌△CFE（SAS)

∴AD=CF（全等三角形对应边相等）

∠ADE=∠F（全等三角形对应角相等）

∴BD∥CF（内错角相等，两直线平行）

∵AD=BD

∴BD=CF

∴四边形BCFD是平行四边形

∴DE//BC，DE=1/2DF=1/2BC

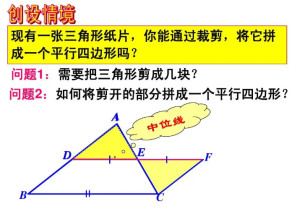中位线定理(3)已知△ABC中，D、E分别是AB、AC两边中点。

求证DE平行于BC且等于BC/2

方法一：几何法

过C作AB的平行线交DE的延长线于G点。

∵CG∥AD

∴∠A=∠ACG

∵∠AED=∠CEG、AE=CE、∠A=∠ACG（用大括号）

∴△ADE≌△CGE （A.S.A)

∴AD=CG（全等三角形对应边相等）

∵D为AB中点

∴AD=BD

∴BD=CG

又∵BD∥CG

∴BCGD是平行四边形（一组对边平行且相等的四边形是平行四边形）

∴DG∥BC且DG=BC

∵△ADE≌△CGE （A.S.A)

∴DE=GE

∴DE=DG/2=BC/2

∴三角形的中位线定理成立

方法二：坐标法

设三角形三点分别为（x1，y1），（x2，y2），（x3，y3）

则一条边长为 ：根号（x2-x1）^2+(y2-y1）²

另两边中点为（（x1+x3）/2，（y1+y3）/2），和（(x2+x3）/2，（y2+y3）/2）

这两中点距离为：根号（（x2+x3）/2-(x1+x3）/2）^2+((y2+y3）/2-(y1+y3）/2）^2

最后化简时将x3，y3消掉正好中位线长为其对应边长的一半

方法三

延长DE到点G，使EG=DE，连接CG

∵点E是AC中点

∴AE=CE

∵AE=CE、∠AED=∠CEF、DE=GE

∴△ADE≌△CGE (S.A.S)

∴AD=CG、∠G=∠ADE

∵D为AB中点

∴AD=BD

∴BD=CG

∵点D在边AB上

∴DB∥CG

∴BCGD是平行四边形

∴DE=DG/2=BC/2

∴三角形的中位线定理成立

方法四：向量DE=DA+AE=(BA+AC)/2=BC/2

∴DE//BC且DE=BC/2^[3]