- 小样本理论

小样本理论
简介
创立者
小样本理论和方法的创立者是威廉.西利.戈塞特(William Sealy Gosset,1876-1937),他是英国统计学家,是现代统计方法及其应用于实验设计与分析的先驱。[1]
形成背景
小样本理论的系统形成,是19世纪初叶的事情。小样本分布在统计假设检验和区间估计等方面的应用,可以省人、省钱、省时间,因而,引起了工业、农业和科学研究等实际工作者的重视和欢迎;同时,也吸引更多的统计学家开拓这方面新的领域,这样便推动着小样本理论及其应用不断地向纵深发展。[2]
容量标准
当样本容量 n<50 的时侯,构造统计量一般不能借助于大样本理论。这时,统计量的分布为与正态分布不同的新分布,于是产生小样本分布的理论。[2]
常见分布
在小样本理论里,最常见的分布有:t 分布,![]() 分布和 F 分布。一般说来,从正态总体里,随机抽取容量为(n<50)的样本
分布和 F 分布。一般说来,从正态总体里,随机抽取容量为(n<50)的样本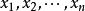 ,构造
,构造![]() 变量,
变量,![]() 变量和 F 变量等统计量,研究这些统计量的概率分布和性质等,形成了小样本统计方法的系统理论。[2]
变量和 F 变量等统计量,研究这些统计量的概率分布和性质等,形成了小样本统计方法的系统理论。[2]
定义
小样本理论是样本理论的一个分支,样本分布与样本的数量 n 有关,小样本理论是讨论样本数 n 较小的样本分布问题。[3]
小样本理论(small sample theory)亦称精确样本理论,统计量性质的一种刻画,它研究样本容量固定时,各种统计量的性质及由此进行的统计推断。精确样本理论最早的例子是由英国统计学家和化学家戈塞特(Gossett , W. S.)于1908年提出的 t 分布。
理论系统
卡方分布
设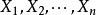 独立同分布于标准正态分布
独立同分布于标准正态分布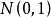 ,则
,则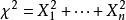 的分布称为自由度为 n 的卡方分布,记作
的分布称为自由度为 n 的卡方分布,记作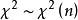 。[4]
。[4]
若随机变量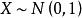 ,则
,则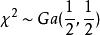 ,根据伽马分布的可加性有
,根据伽马分布的可加性有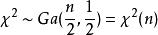 ,由此可见
,由此可见![]() 分布是伽马分布的特例。
分布是伽马分布的特例。
(1)![]() 分布的密度函数的图像是一个只取非负值的偏态分布,其具体表达式为:
分布的密度函数的图像是一个只取非负值的偏态分布,其具体表达式为:
![]()
(2)它的期望等于自由度,方差等于2倍自由度,即:
![]()
F分布
设随机变量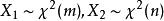 ,其中
,其中![]() 独立,则称
独立,则称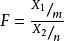 的分布是自由度为 m 与 n 的 F 分布,记作
的分布是自由度为 m 与 n 的 F 分布,记作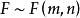 ,其中 m 称为分子自由度,n 称为分母自由度。
,其中 m 称为分子自由度,n 称为分母自由度。
(1)F 分布的密度函数是一个只取非负值的偏态分布,表达式为:
![]()
(2)当随机变量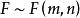 时,对给定
时,对给定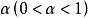 ,称满足概率等式
,称满足概率等式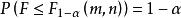 的
的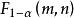 是自由度为 m 与 n 的 F 分布
是自由度为 m 与 n 的 F 分布![]() 分位数;
分位数;
(3)由 F 分布的构造可知,若 则有
则有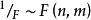 。[4]
。[4]
t分布
设随机变量![]() 独立,且
独立,且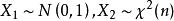 ,则称
,则称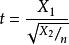 的分布为自由度为 n 的 t 分布,记为:
的分布为自由度为 n 的 t 分布,记为: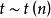 。
。
(1)t 分布的密度函数的图像是一个关于纵轴对称的分布,与标准正态分布的密度函数形状类似,只是峰比标准正态分布低一些,尾部的概率比标准正态分布大一些;自由度为 n 的 t 分布密度函数的具体表达式为:
![]()
(2)自由度为1的 t 分布就是标准柯西分布,它的均值不存在;
(3)n>1 时,t 分布的数学期望存在且为0;
(4)n>2 时,t 分布的方差存在,且为![]() ;
;
(5) 当自由度较大(如![]() )时,t 分布可以用
)时,t 分布可以用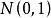 分布近似。[4]
分布近似。[4]
 收藏
收藏

-
柯明斯基理论 第三季
2025-11-01 08:58:29 查看详情


 求购
求购








