平行线分线段成比例定理

平行线分线段成比例亦称平行截割定理，平面几何术语，指三条平行线截两条直线，所得的四条线段对应成比例，如图1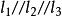，，则

平行截割定理是研究相似形最常用的一个性质，它的重要特例：在一直线上截得相等线段的一组平行线，也把其他直线截成相等的线段，称其为平行线等分线段。^[2]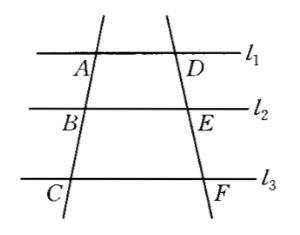图1

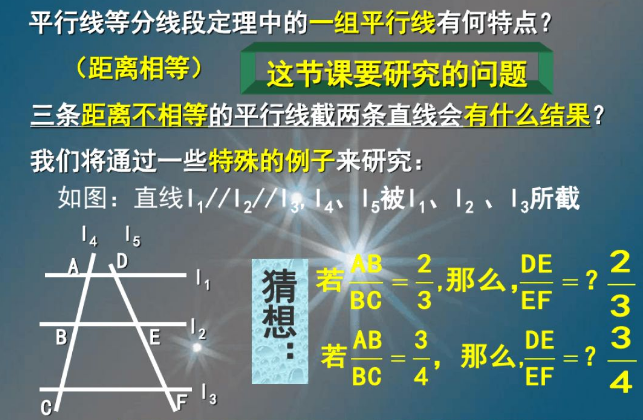平行线分线段成比例定理(3)设三条平行线与直线 m 交于 A、B、C 三点，与直线 n 交于 D、E、F 三点。

连结AE、BD、BF、CE

根据平行线的性质可得 S△ABE=S△DBE， S△BCE=S△BEF，

∴S△ABE/S△CBE=S△DBE/S△BFE

根据不同底等高三角形面积比等于底的比可得：AB/BC=DE/EF。

由更比性质、等比性质得：AB/DE=BC/EF=(AB+BC)/(DE+EF)=AC/DF。

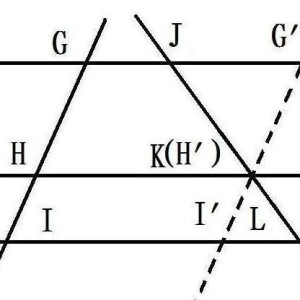平行线分线段成比例定理过一点的一线束被平行线截得的对应线段成比例。

平行于三角形一边的直线截其它两边（或两边的延长线）所得对应线段成比例。

平行于三角形一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形的三边对应成比例。

平行线分线段成比例定理：

三条平行线截两条直线，所得对应线段成比例。

推广：过一点的一线束被平行线截得的对应线段成比例。

定理推论：

①平行于三角形一边的直线截其它两边（或两边的延长线）所得对应线段成比例。

②平行于三角形一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形的三边对应成比例。