合比性质

在一个比例里，第一个比的前后项的和与它后项的比，等于第二个比的前后项的和与它的后项的比，这称为比例中的合比定理，这种性质称为合比性质。

用字母表达为：若a/b=c/d，则(a±kb)/b=(c±kd)/d（b≠0、d≠0）

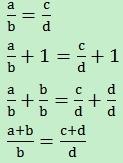书写版推导表达当b≠0且d≠0时

a/b=c/d

a/b±k=c/d±k

a/b±kb/b=c/d±kd/d

(a±kb)/b=(c±kd)/d

分比性质：

在一个比例里，第一个比的前后项的差与它的后项的比，等于第二个比的前后项的差与它们的后项的比。

字母表达：若a/b=c/d,则(a-b)/b=(c-d)/d （b≠0、d≠0）

合分比性质：

在一个比例里，第一个比的前后项的和与它的前后项的差的比，等于第二个比的前后项的和与它的前后项的差的比。

字母表达：若a/b=c/d,则(a+b)/(a-b)=(c+d)/(c-d)（a≠b,c≠d,b≠0,d≠0）

等比性质：

若a1/b1=a2/b2=a3/b3=...=an/bn

则a1/b1=a2/b2=...=(a1+a2+a3+...+an)/(b1+b2+b3+...+bn)=an/bn

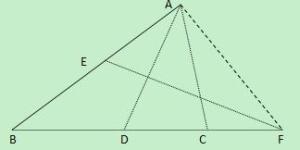例题图如图，在△ABC中，AD为∠BAC的角平分线，EF是AD的垂直平分线且交AB于E，交BC的延长线于F，求证：DC·DF=BD·CF分析：

欲证：DC·DF=BD·CF

即证：DC/CF=BD/DF

即证：(DC+CF)/CF=(BD+DF)/DF （等式两边加上1）

若连结AF，则AF=DF

故即证：AF/CF=BF/AF

只需证△FAB∽△FCA

证明：

连结AF，则AF=DF，∠FAD=∠FDA

∵AD平分∠BAC

∴∠BAD=∠CAD

∴AF=DF

∴∠FDA=∠FAD

又∵∠FAD=∠CAD+∠CAF，∠FDA=∠B+∠BAD

∴∠B=∠CAF

∴△FAB∽△FCA。