双曲抛物面

双曲抛物面又称马鞍面，它在笛卡儿坐标系中的方程为：^[2]

其中x、y、z是平面直角坐标系三个坐标轴方向上的变量，a、b是常数。

如果把双曲抛物面

顺着+z的方向旋转π/4的角度，则方程为：

如果，则简化为：.

最后，设，我们可以看到双曲抛物面

与以下的曲面是全等的：

因此它可以视为乘法表的几何表示。

用平面截此曲面，^[3]所得截痕l为平面上的抛物线，此抛物线开口向下，其顶点坐标为。当t变化时，l的形状不变，位置只作平移，而l的顶点的轨迹L为平面y=0上的抛物线。因此，以l为母线，L为准线，母线l的顶点在准线L上滑动，且母线作平行移动，这样得到的曲面便是双曲抛物面。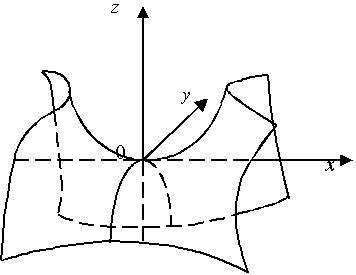图1.双曲抛物面