- 辐角

辐角
中文名
辐角
方向规定
逆时针为正,顺时针为负
定义
 由于一个复数
由于一个复数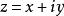 可以由有序实数对
可以由有序实数对![]() 唯一确定,而有序实数对与平面直角坐标系
唯一确定,而有序实数对与平面直角坐标系![]() 中的点一一对应,因此可以用坐标为
中的点一一对应,因此可以用坐标为![]() 的点
的点![]() 来表示该复数,此时
来表示该复数,此时![]() 轴上的点与实数对应,称
轴上的点与实数对应,称![]() 轴为实轴,
轴为实轴,![]() 轴上的点(除原点外)与纯虚数对应,称
轴上的点(除原点外)与纯虚数对应,称![]() 轴为虚轴,像这样表示复数的平面称为复平面。
轴为虚轴,像这样表示复数的平面称为复平面。
复数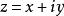 还可以用向量
还可以用向量![]() 来表示,
来表示,![]() 与
与![]() 分别是向量
分别是向量![]() 在
在![]() 轴与
轴与![]() 轴上的投影。这样,复数
轴上的投影。这样,复数![]() 就与平面上的向量
就与平面上的向量![]() 建立了一一对应的关系。
建立了一一对应的关系。
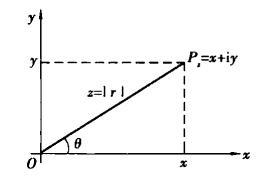
 向量
向量![]() 的长度称为复数的模或绝对值,记作
的长度称为复数的模或绝对值,记作![]() ,于是
,于是
![]()
当点![]() 不是原点,即复数
不是原点,即复数![]() 时,向量
时,向量![]() 与
与![]() 轴正向的夹角称为复数
轴正向的夹角称为复数![]() 的辐角,记作
的辐角,记作![]() 。辐角的符号规定为:由正实轴依反时针方向转到
。辐角的符号规定为:由正实轴依反时针方向转到![]() 为正,依顺时针方向转到
为正,依顺时针方向转到![]() 为负。[1]
为负。[1]
辐角主值
显然一个非零复数![]() 的辐角有无穷多个值,它们相差
的辐角有无穷多个值,它们相差![]() 的整数倍,但
的整数倍,但![]() 中只有一个值
中只有一个值![]() 满足条件
满足条件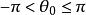 ,称
,称![]() 为复数
为复数![]() 的主辐角,记为
的主辐角,记为![]() ,于是
,于是
![]()
当![]() 时,
时,![]() 的辐角没有意义。
的辐角没有意义。
复数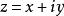 的主辅角
的主辅角![]() 与反正切的主值
与反正切的主值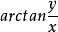 有以下关系:[1]
有以下关系:[1]

三角表示式和指数表示式
由直角坐标与极坐标的关系可知,非零有穷复数![]() 可以用其模
可以用其模![]() 与辐角
与辐角![]() 来表示,即
来表示,即
![]()
利用欧拉公式
![]()
得
![]()
分别称上述第一式和第三式为非零复数![]() 的三角表示式和指数表示式,这三种表示式可以和代数表示式之间互相转化,以方便讨论不同问题时的需要。[1]
的三角表示式和指数表示式,这三种表示式可以和代数表示式之间互相转化,以方便讨论不同问题时的需要。[1]

相关百科


 求购
求购







