- 圆幂定理

圆幂定理
发展简史
圆幂定理是一个总结性的定理,是对相交弦定理、切割线定理及割线定理(切割线定理推论)以及它们推论的统一与归纳。[1]根据两条与圆有相交关系的线的位置不同,有以下定理:
- 相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。
- 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
- 割线定理:从圆外一点P引两条割线与圆分别交于A、B;C、D,则有PA·PB=PC·PD
从上述定理可以看出,两条线的位置从内到外,都有着相似的结论。经过总结和归纳,便得出了圆幂定理。
点对圆的幂
定义
P点对圆O的幂定义为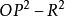
性质
点P对圆O的幂的值,和点P与圆O的位置关系有下述关系:
- 点P在圆O内→P对圆O的幂为负数;
- 点P在圆O外→P对圆O的幂为正数;
- 点P在圆O上→P对圆O的幂为0。
注意:以上关系除正向应用通过点和圆的位置关系判断点对的圆的幂的符号,还可以逆向应用,通过点对圆的幂的符号反推点和圆的位置关系。[1]
在某些书中,点P对圆O的幂表示为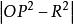
定理证明
图Ⅰ:相交弦定理。如图,AB、CD为圆O的两条任意弦。相交于点P,连接AD、BC,由于∠B与∠D同为弧AC所对的圆周角,因此由圆周角定理知:∠B=∠D,同理∠A=∠C,所以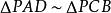 。所以有:
。所以有: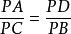 ,即:
,即: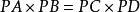 。
。
图Ⅱ:割线定理。如图,连接AD、BC。可知∠B=∠D,又因为∠P为公共角,所以有
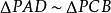 ,同上证得
,同上证得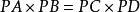 。
。
图Ⅲ:切割线定理。如图,连接AC、AD。∠PAC为切线PA与弦AC组成的弦切角,因此有∠PBC=∠D,又因为∠P为公共角,所以有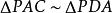 ,易证
,易证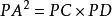
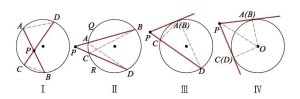 圆幂定理的所有情况图Ⅳ:切线长定理。PA、PC均为切线,则∠PAO=∠PCO=90°,在直角三角形中:OC=OA=R,PO为公共边,因此
圆幂定理的所有情况图Ⅳ:切线长定理。PA、PC均为切线,则∠PAO=∠PCO=90°,在直角三角形中:OC=OA=R,PO为公共边,因此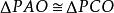 。所以PA=PC,所以
。所以PA=PC,所以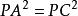 。
。
综上可知,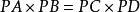 是普遍成立的。[3]
是普遍成立的。[3]

相关百科


 求购
求购







