γ跃迁

 γ光子(或称γ射线)-内部结构模型图　　γtransition 又称γ衰变，原子核通过发射γ光子(或称γ射线) 从激发态跃迁到较低能态的过程。γ跃迁的性质与跃前后能级的性质有关，通过对它的研究，可以了解原核能级特性及原子核反应机制。γ光子的能量等于跃迁前后核能级能量之差，在电子伏到兆电子伏之间。γ跃迁的多极性指γ跃迁的电磁性质和辐射的极级，是γ跃迁的重要特性之一。通常用符号E 表示跃迁，用符号 M表示磁跃迁。

　　原子核通过自发电磁过程从激发态跃迁到较低能态释放其过剩能量的核衰变过程。又称γ衰变。γ跃迁时，核的成分不变，即核的电荷数和质量数不变。γ跃迁的方式分γ发射和内电子转换。

　　①γ发射。γ跃迁过程中发射γ光子，γ光子的能量等于跃迁前后核能级能量差，在千电子伏特（keV）到兆电子伏特（MeV）之间，相应的波长在X射线之下。γ发射是电磁作用过程，核内电荷分布和电流分布发生变化，电荷分布由电偶极矩，电四极矩等描述，电流分布由磁偶极矩、磁四极矩等描述。γ发射具有多极性，通常用E1、E2、E3表示电多极跃迁，用M1、M2、M3表示磁多极跃迁。γ发射过程遵从能量守恒、角动量守恒、宇称守恒。根据这些守恒定律可得出核能级γ发射的选择定则，从而根据已知跃迁的多极性和始末态中一个能级的自旋和宇称，可推出只一能级的自旋和宇称，这是核谱学的一项重要工作。

　　②内电子转换。原子核内的非辐射跃迁。不稳定核从高能态跃迁到低能态时不发射γ光子，而是通过原子核的电磁场同内层电子相互作用，直接把跃迁能量交给内层电子，造成内层电子发射。依照来自K、L、M等不同壳层发射电子，相应称为 K、L、M等转换。内转换对重核的低能级显得很重要。当核激发能超过一对电子的静能2mec2约为1.02MeV时，可内转换放出一对正负电子。

　　发生γ跃迁的不稳定核常常是a衰变或β衰变的产物，有的是其他核反应过程的产物。γ跃迁的半衰期相对说来比α衰变或β衰变要短得多。

　　辐射带走的宇称和角动量量子数的奇偶性相同的为电多极辐射，相反的为磁多极辐射。因此，电多极辐射的宇称为(-1)L，磁多极辐射的宇称为(-1)L+1。 由辐射的角动量和宇称可定出γ跃迁的多极性，反之亦然。研究γ跃迁的重要任务之一是从实验定出γ跃迁的多极性，以检验理论的正确性。

　　由多极辐射理论，可以得到电2L极辐射的跃迁几率λE(L)和磁2L极辐射的跃迁几率λM(L)的公式如下

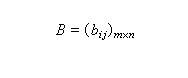
公式

　　子能量Eγ的关系是：

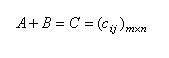公式

　　由上面公式可见，跃迁能量越大，γ跃迁几率也越大。

　　实验上可以通过测量γ衰变的半衰期或平均寿命求得γ跃迁几率，以便和理论进行比较。

公式

　　根据宇称守恒定律，光子带走的宇称πγ由下式决定

公式

　　另外,关于跃迁几率数量级的比较,有下面三点结论：①同级的电跃迁几率大于磁跃迁几率；②多极级越低，跃迁几率越大；③一般讲,磁2L极的跃迁几率与电2L+1极的跃迁几率有相同的数量级。 由上述角动量守恒和宇称守恒的讨论以及跃迁几率数量级的比较,可以得出始态(Ii，πi)到末态(If，πf)的跃迁选择定则，如表所示。表中ΔI和Δπ分别表示始末态自旋角动量和宇称的变化，括号内的跃迁多极性表示有可能与括号前的跃迁同时出现。 根据跃迁选择定则，可以从始末态的自旋和宇称定出几率最大的跃迁多极性。例如，2+→0+跃迁的多极性为E2，4-→2+跃迁的多极性为M2(E3)。 γ跃迁

　　如果已知跃迁的多极性和始末态中一个能级的自旋和宇称，由选择定则可以推出另一能级的自旋和宇称。不过这样定出的能级自旋一般有两种或三种可能值，需配合其他数据以后，才能肯定其中之一。由实验测得的跃迁多极性推出能级的自旋和宇称，是核谱学的一项重要内容。

　　另外，如果核初始处于比较高的激发态，由角动量守恒和宇称守恒的讨论及跃迁几率数量级的比较，可知道它往往不能直接跃迁到基态，而要经过一系列的中间态间跃迁，这种多次相联的γ跃迁称为级联γ跃迁。

　　内转换电子的能量E＝Eγ-Be,其中Eγ为核的跃迁能量，Be为该电子的结合能。

　　在相同始末态之间的跃迁,发出第L壳层内转换电子的几率λe(L)与发出γ射线的几率λγ之比，定义为该壳层内转换系数α(L)

公式

　　如K壳层内转换系数 。

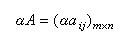公式

　　α＝α(K)+α(L)+α(M)+…。

　　理论分析表明,内转换系数基本上只同跃迁能量、核电荷数Z、跃迁多极性以及内转换电子所在壳层有关,而同核波函数相关的矩阵元无关，因而可以对它进行比较精确的计算。大致说来，Z增大，α增加很快；随着跃迁能量增加,α减小；L大，α也大。因此内转换对重原子核的低能级显得很重要。通过对内转换系数的测量，可以很好地定出跃迁的多极性，从而确定有关能级的自旋和宇称。