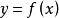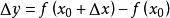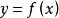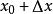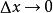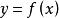- 对数导数

对数导数
定义
设函数在点及其附近有定义,当自变量x在处有改变量(可正可负),则函数y相应地有改变量,这两个改变量的比叫做函数在到之间的平均变化率.
如果当时,有极限,我们就说函数在点处可导,这个极限叫做在点处的导数(即瞬时变化率,简称变化率),记作![]() 。
。
函数![]() 在点
在点![]() 处的导数就是函数平均变化率当自变量的改变量趋向于零时的极限.如果极限不存在,我们就说函数
处的导数就是函数平均变化率当自变量的改变量趋向于零时的极限.如果极限不存在,我们就说函数![]() 在点
在点![]() 处不可导。
处不可导。
求导方法
由导数定义,我们可以得到求函数![]() 在点
在点![]() 处的导数的方法[1][1]:
处的导数的方法[1][1]:
(1)求函数的增量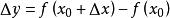 ;
;
(2)求平均变化率;
(3)取极限,得导数;
几何意义
函数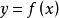 在点
在点![]() 处的导数的几何意义,就是曲线
处的导数的几何意义,就是曲线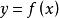 在点
在点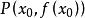 处的切线的斜率
处的切线的斜率![]() 。
。
相应地,切线方程为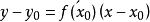 。
。
常见函数导数
函数![]() (C为常数)的导数
(C为常数)的导数![]() .[2]
.[2]
函数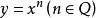 的导数
的导数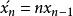 .
.
函数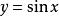 的导数
的导数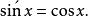
函数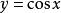 的导数
的导数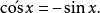
求导法则
和的导数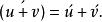
差的导数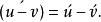
积的导数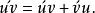
复合函数求导法则
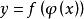 一般地,复合函数]对自变量x的导数
一般地,复合函数]对自变量x的导数![]() ,等于已知函数对中间变量
,等于已知函数对中间变量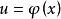 的导数
的导数![]() ,乘以中间变量u对自变量x的导数。
,乘以中间变量u对自变量x的导数。
对数、指数函数的导数
导数又叫微商,是因变量的微分和自变量微分之商;给导数取积分就得到原函数(其实是原函数与一个常数之和

相关百科


 求购
求购