- 伽玛函数

伽玛函数
函数简介
伽玛函数(Gamma Function)作为阶乘的延拓,是定义在复数范围内的亚纯函数,通常写成![]() 。
。
(1)在实数域上伽玛函数定义为:
![]()
(2)在复数域上伽玛函数定义为:
![]()
其中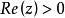 ,此定义可以用解析开拓原理拓展到整个复数域上,非正整数除外。
,此定义可以用解析开拓原理拓展到整个复数域上,非正整数除外。
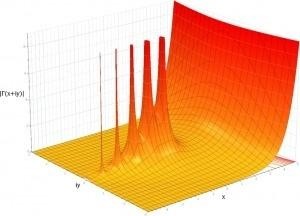 复平面上的Gamma 函数
复平面上的Gamma 函数
(3)除了以上定义之外,伽马函数公式还有另外一个写法:
![]()
我们都知道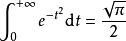 是一个常用积分结果,公式(3)可以用
是一个常用积分结果,公式(3)可以用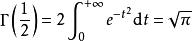 来验证。
来验证。
(4)伽马函数还可以定义为无穷乘积:
![]()
不完全gamma函数
详见不完全伽马函数
历史背景
1728年,哥德巴赫在考虑数列插值的问题,通俗的说就是把数列的通项公式定义从整数集合延拓到实数集合,例如数列1,4,9,16.....可以用通项公式n²自然的表达,即便 n 为实数的时候,这个通项公式也是良好定义的。直观的说也就是可以找到一条平滑的曲线y=x²通过所有的整数点(n,n²),从而可以把定义在整数集上的公式延拓到实数集合。一天哥德巴赫开始处理阶乘序列1,2,6,24,120,720,...,我们可以计算2!,3!,是否可以计算2.5!呢?我们把最初的一些(n,n!)的点画在坐标轴上,确实可以看到,容易画出一条通过这些点的平滑曲线。

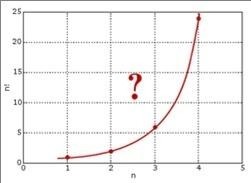
但是哥德巴赫无法解决阶乘往实数集上延拓的这个问题,于是写信请教尼古拉斯·伯努利和他的弟弟丹尼尔·伯努利,由于欧拉当时和丹尼尔·伯努利在一块,他也因此得知了这个问题。而欧拉于1729 年完美地解决了这个问题,由此导致了伽玛 函数的诞生,当时欧拉只有22岁。
函数性质
1、通过分部积分的方法,可以推导出这个函数有如下的递归性质:
Γ(x+1)=xΓ(x)
于是很容易证明,伽马函数可以当成是阶乘在实数集上的延拓,对于正整数n,具有如下性质:
![]()
2、与贝塔函数的关系:
![]()
3、在概率的研究中有一个重要的分布叫做伽玛分布:
![]()
其中![]() 。
。
4、对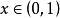 ,有
,有
![]()
这个公式称为余元公式。
由此可以推出以下重要的概率公式:![]()
5、对于![]() ,伽马函数是严格凹函数。
,伽马函数是严格凹函数。
6、伽马函数是亚纯函数,在复平面上,除了零和负整数点以外,它全部解析,而伽马函数在![]() 处的留数为
处的留数为
![]()
Stirling公式
 伽玛函数(3)Gamma 函数从它诞生开始就被许多数学家进行研究,包括高斯、勒让德、魏尔斯特拉斯、刘维尔等等。这个函数在现代数学分析中被深入研究,在概率论中也是无处不在,很多统计分布都和这个函数相关。Gamma 函数作为阶乘的推广,首先它也有和 Stirling 公式类似的一个结论:即当x取的数越大,Gamma 函数就越趋向于 Stirling 公式,所以当x足够大时,可以用Stirling 公式来计算Gamma 函数值。
伽玛函数(3)Gamma 函数从它诞生开始就被许多数学家进行研究,包括高斯、勒让德、魏尔斯特拉斯、刘维尔等等。这个函数在现代数学分析中被深入研究,在概率论中也是无处不在,很多统计分布都和这个函数相关。Gamma 函数作为阶乘的推广,首先它也有和 Stirling 公式类似的一个结论:即当x取的数越大,Gamma 函数就越趋向于 Stirling 公式,所以当x足够大时,可以用Stirling 公式来计算Gamma 函数值。
![]()
函数内容
伽玛函数的对数的导数称为Digamma函数,记为
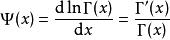 。
。
Digamma函数同调和级数相关,其中
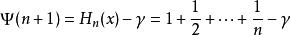
其中
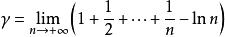
是欧拉常数。
而对于任意x有
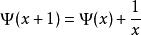
在复数范围内,Digamma函数可以写成
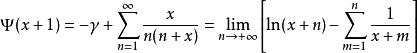
而Digamma函数的泰勒展开式为
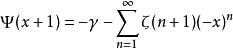
其中函数![]() 为黎曼zeta函数,是关于黎曼猜想的一个重要函数。
为黎曼zeta函数,是关于黎曼猜想的一个重要函数。
类似伽玛函数,Digamma函数可以有渐进式:
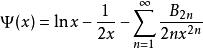
积分形式
![]()
digamma值
![]()
![]()
![]()
![]()
![]()
![]()
![]()
函数应用
在Matlab中的应用
其表示N在N-1到0范围内的整数阶乘。
公式为:gamma(N)=(N-1)*(N-2)*...*2*1
例如:
gamma(6)=5*4*3*2*1
ans=120

-
1641函数信号发生器
2025-11-01 01:56:16 查看详情


 求购
求购










