- 一元三次方程

一元三次方程
解法
 一元三次方程(6)卡尔丹公式法的特殊情况
一元三次方程(6)卡尔丹公式法的特殊情况
一元三次方程都可化为x³+px+q=0。它的解是:

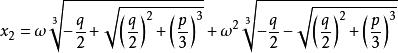

其中 。
。
根与系数的关系为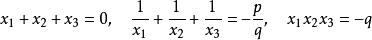 。
。
判别式为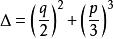 。当
。当![]() 时,有一个实根和两个复根;
时,有一个实根和两个复根;![]() 时,有三个实根,当
时,有三个实根,当 时,有一个三重零根,
时,有一个三重零根,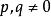 时,三个实根中有两个相等;
时,三个实根中有两个相等;![]() 时,有三个不等实根。
时,有三个不等实根。
三个根的三角函数表达式(仅当![]() 时)为
时)为

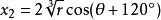

其中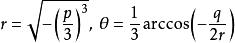 。
。
卡丹公式法的一般情况
一般的一元三次方程可写成 的形式。上式除以
的形式。上式除以![]() ,并设
,并设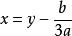 ,则可化为如下形式:
,则可化为如下形式:
 ,其中
,其中 ,
, 。
。
 标准型方程中卡尔丹公式的一个实根可用特殊情况的公式解出
标准型方程中卡尔丹公式的一个实根可用特殊情况的公式解出 ,则原方程的三个根为
,则原方程的三个根为
 。
。
三个根与系数的关系为
 。
。
盛金公式法
三次方程应用广泛。用根号解一元三次方程,虽然有著名的卡尔丹公式,并有相应的判别法,但使用卡尔丹公式解题比较复杂,缺乏直观性。范盛金推导出一套直接用a、b、c、d表达的较简明形式的一元三次方程的一般式新求根公式——盛金公式,并建立了新判别法——盛金判别法。
1.盛金公式
一元三次方程aX3+bX2+cX+d=0,(a,b,c,d∈R,且a≠0)
重根判别式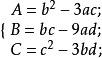
总判别式Δ=B2-4AC。
当A=B=0时,
盛金公式1:
 当Δ=B2-4AC>0时,
当Δ=B2-4AC>0时,
盛金公式2:


盛金公式2的三角式:

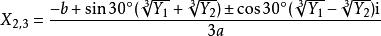
其中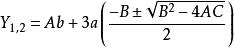 ,
,![]() 。
。
当Δ=B2-4AC=0时,
盛金公式3:
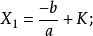

其中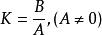 。
。
当Δ=B2-4AC<0时,
盛金公式4:


其中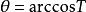 ,
,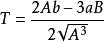 (A>0,-1<T<1)。
(A>0,-1<T<1)。
2.盛金判别法
当A=B=0时,方程有一个三重实根。
当Δ=B2-4AC>0时,方程有一个实根和一对共轭虚根。
当Δ=B2-4AC=0时,方程有三个实根,其中有一个二重根。
当Δ=B2-4AC<0时,方程有三个不相等的实根。
3.盛金定理
当b=0,c=0时,盛金公式1无意义;当A=0时,盛金公式3无意义;当A≤0时,盛金公式4无意义;当T<-1或T>1时,盛金公式4无意义。
当b=0,c=0时,盛金公式1是否成立?盛金公式3与盛金公式4是否存在A≤0的值?盛金公式4是否存在T<-1或T>1的值?盛金定理给出如下回答:
盛金定理1:当A=B=0时,若b=0,则必定有c=d=0(此时,方程有一个三重实根0,盛金公式1仍成立)。
盛金定理2:当A=B=0时,若b≠0,则必定有c≠0(此时,适用盛金公式1解题)。
盛金定理3:当A=B=0时,则必定有C=0(此时,适用盛金公式1解题)。
盛金定理4:当A=0时,若B≠0,则必定有Δ>0(此时,适用盛金公式2解题)。
盛金定理5:当A<0时,则必定有Δ>0(此时,适用盛金公式2解题)。
盛金定理6:当Δ=0时,若A=0,则必定有B=0(此时,适用盛金公式1解题)。
盛金定理7:当Δ=0时,若B≠0,盛金公式3一定不存在A≤0的值(此时,适用盛金公式3解题)。
盛金定理8:当Δ<0时,盛金公式4一定不存在A≤0的值。(此时,适用盛金公式4解题)。
盛金定理9:当Δ<0时,盛金公式4一定不存在T≤-1或T≥1的值,即T出现的值必定是-1<T<1。
显然,当A≤0时,都有相应的盛金公式解题。
注意:盛金定理逆之不一定成立。如:当Δ>0时,不一定有A<0。
盛金定理表明:盛金公式始终保持有意义。任意实系数的一元三次方程都可以运用盛金公式直观求解。
以上结论,发表在《海南师范学院学报(自然科学版)》(第2卷,第2期;1989年12月,中国海南。国内统一刊号:CN46-1014),第91—98页。范盛金,一元三次方程的新求根公式与新判别法。(NATURAL SCIENCE JOURNAL OF HAINAN TEACHERES COLLEGE,Hainan Province,China. Vol. 2,No. 2;Dec,1989),A new extracting formula and a new distinguishing means on the one variable cubic equation., Fan Shengjin. PP·91—98 .
通用求根公式
当一元三次方程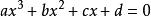 的系数是复数时,直接使用卡丹公式求解,有时会出现问题。此时,可使用下面的公式:
的系数是复数时,直接使用卡丹公式求解,有时会出现问题。此时,可使用下面的公式:


当 时
时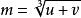
当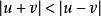 时
时
当![]() 时
时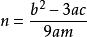
当![]() 时
时![]()
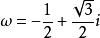
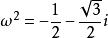
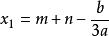

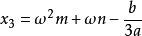
另一种解法:
先把一般的一元三次方程化为特殊的一元三次方程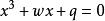 ,令
,令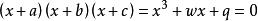
由一元三次方程的 韦达定理可得: 带入
带入 可得
可得 且
且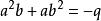 ,令
,令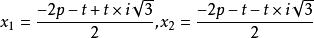 ,(其中
,(其中![]() ,p与t均为未知数)为一元三次方程
,p与t均为未知数)为一元三次方程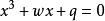 的两根。
的两根。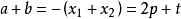 ,
,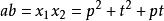 ,则
,则 ,
,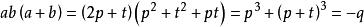 . 把
. 把 带入可得
带入可得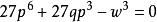 .求出p,t再求出
.求出p,t再求出![]() 与
与![]() 即可。此法的优点是求出的x不会出现有增根的情况,缺点但是会有重根。
即可。此法的优点是求出的x不会出现有增根的情况,缺点但是会有重根。
计算程序代码
通用求根公式(VC++)
| #include <math.h>#include <complex>/***************************************************************\对复数 x 开 n 次方\***************************************************************/std::complex<double> sqrtn(const std::complex<double>&x,double n){double r = _hypot(x.real(),x.imag()); //模if(r > 0.0){//模不为零时,开方double a = atan2(x.imag(),x.real()); //辐角n = 1.0 / n;r = pow(r,n);a *= n;return std::complex<double>(r * cos(a),r * sin(a));}return std::complex<double>(); //模为零时,返回零}/***************************************************************\求解一元三次方程 a*x^3 + b*x^2 + c*x + d = 0\***************************************************************/void CubicEquation(std::complex<double> x[3],std::complex<double> a,std::complex<double> b,std::complex<double> c,std::complex<double> d){a = 1.0 / a;b *= a;c *= a;d *= a;std::complex<double> u = ((9.0 * c - 2.0 * b * b) * b - 27.0 * d) / 54.0;std::complex<double> v = 3.0 * ((4.0 * c - b * b) * c * c+ ((4.0 * b * b - 18.0 * c) * b + 27.0 * d) * d);v = sqrtn(v,2.0) / 18.0;std::complex<double> m = u + v;std::complex<double> n = u - v;if(n.real() * n.real() + n.imag() * n.imag() >m.real() * m.real() + m.imag() * m.imag()){m = n;}a = b/-3.0;if(m.real() * m.real() + m.imag() * m.imag() > 0.0){m = sqrtn(m,3.0);n = (b * b - 3.0 * c) / (9.0 * m);std::complex<double>o1(-0.5,+0.86602540378443864676372317075294);std::complex<double>o2(-0.5,-0.86602540378443864676372317075294);x[0] = m + n + a;x[1] = o1 * m + o2 * n + a;x[2] = o2 * m + o1 * n + a;}else{x[0] =x[1] =x[2] = a;}} |
验算代码(VC++)
| std::complex<double> x[3];std::complex<double> x1(1.0,0.0); //随便填std::complex<double> x2(2.0,0.0); //随便填std::complex<double> x3(3.0,0.0); //随便填std::complex<double> a (4.5,0.0); //随便填(不为零即可)std::complex<double> b = a * (-x1-x2-x3);std::complex<double> c = a * (x2 * x3 + x1 * x3 + x1 * x2);std::complex<double> d = a * (-x1 * x2 * x3);CubicEquation(x,a,b,c,d); |
解方程故事
| #include <math.h>#include <complex>/***************************************************************\对复数 x 开 n 次方\***************************************************************/std::complex<double> sqrtn(const std::complex<double>&x,double n){double r = _hypot(x.real(),x.imag()); //模if(r > 0.0){//模不为零时,开方double a = atan2(x.imag(),x.real()); //辐角n = 1.0 / n;r = pow(r,n);a *= n;return std::complex<double>(r * cos(a),r * sin(a));}return std::complex<double>(); //模为零时,返回零}/***************************************************************\求解一元三次方程 a*x^3 + b*x^2 + c*x + d = 0\***************************************************************/void CubicEquation(std::complex<double> x[3],std::complex<double> a,std::complex<double> b,std::complex<double> c,std::complex<double> d){a = 1.0 / a;b *= a;c *= a;d *= a;std::complex<double> u = ((9.0 * c - 2.0 * b * b) * b - 27.0 * d) / 54.0;std::complex<double> v = 3.0 * ((4.0 * c - b * b) * c * c+ ((4.0 * b * b - 18.0 * c) * b + 27.0 * d) * d);v = sqrtn(v,2.0) / 18.0;std::complex<double> m = u + v;std::complex<double> n = u - v;if(n.real() * n.real() + n.imag() * n.imag() >m.real() * m.real() + m.imag() * m.imag()){m = n;}a = b/-3.0;if(m.real() * m.real() + m.imag() * m.imag() > 0.0){m = sqrtn(m,3.0);n = (b * b - 3.0 * c) / (9.0 * m);std::complex<double>o1(-0.5,+0.86602540378443864676372317075294);std::complex<double>o2(-0.5,-0.86602540378443864676372317075294);x[0] = m + n + a;x[1] = o1 * m + o2 * n + a;x[2] = o2 * m + o1 * n + a;}else{x[0] =x[1] =x[2] = a;}} |
词条图册
| std::complex<double> x[3];std::complex<double> x1(1.0,0.0); //随便填std::complex<double> x2(2.0,0.0); //随便填std::complex<double> x3(3.0,0.0); //随便填std::complex<double> a (4.5,0.0); //随便填(不为零即可)std::complex<double> b = a * (-x1-x2-x3);std::complex<double> c = a * (x2 * x3 + x1 * x3 + x1 * x2);std::complex<double> d = a * (-x1 * x2 * x3);CubicEquation(x,a,b,c,d); |

-
非线性方程组数值解法
2025-09-21 00:22:10 查看详情 -
中华人民共和国第十二届全国人民代表大会第三次会议
2025-09-21 00:22:10 查看详情 -
F1方程赛车逆向设计
2025-09-21 00:22:10 查看详情 -
三款小排量小型SUV雪铁龙C3 1.8L车型的油耗方程式
2025-09-21 00:22:10 查看详情 -
成都车展:一汽奔腾无限方程架构发布/第三代B70将问世 e
2025-09-21 00:22:10 查看详情 -
雪铁龙C3 1.8L车型的油耗方程式
2025-09-21 00:22:10 查看详情 -
东风雪铁龙凡尔赛C5 1.8L车型的油耗方程式
2025-09-21 00:22:10 查看详情 -
雪铁龙天逸对比大众途岳 1.8L车型的油耗方程式
2025-09-21 00:22:10 查看详情 -
一元秒杀汽车 疯狂赛车1元秒杀怎么抢
2025-09-21 00:22:10 查看详情


 求购
求购




