帕普斯定理

帕普斯(Pappus)定理:如图，直线l1上依次有点A,B,C，直线l2上依次有点D,E,F，设AE,BD交于P，AF,DC交于Q，BF,EC交于R，则P,Q,R共线。

记PQ与XC交于U,PQ与AZ交于V,只需证明U,V重合，即PU/QU=PV/QV

由 共边比例定理可知，PU/QU=PXC面积/QXC面积(1),QV/PV=QAZ面积/PAZ面积(2)

而PXC面积=(PXC面积/BXC面积)*BXC面积

=(PX/BX)*BXC面积

=(PX*BXC面积)/(BP+PX)

=(AXY面积*BXC面积)/(ABY面积+AXY面积）

=(AXY面积*BXC面积)/ABXY面积

同理，QXC面积=(BCZ面积*XYC面积)/BCZY面积

QAZ面积=(YZC面积*ABZ面积)/BCZY面积

PAZ面积=(ABX面积*AYZ面积)/ABXY面积

以上四式代入(1)(2),得到

(PU/QU)*(QV/PV)

=(AXY面积/AYZ面积)*(BXC面积/ABX面积)*(YZC面积/XYC面积)*(ABZ面积/BCZ面积)

=(XY/YZ)*(BC/AB)*(YZ/XY)*(AB/BC)

=1

故命题得证。

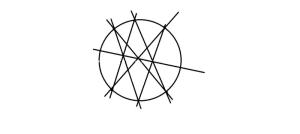帕普斯定理图册(2)由两点A，B各出发三条射线，A1，A2，A3；B1，B2，B3，设过A1，B2交点；A2，B1交点的直线为C1，过A2，B3交点；A3，B2交点的直线为C2，过A1，B3交点；A3，B1交点的直线为C3,则C1,C2,C3共点。

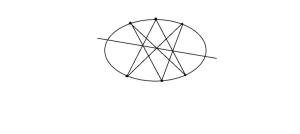
此定理在圆中依然成立，圆中以任一直径为界线，直径两侧分别取A1，A2，A3；B1，B2，B3。连接A1，B2；A1，B3。A2,B1;A2,B3。A3,B1;A3,B2.则A1B2,A2B1交于C1；A1B3，A3B1交于C2；A2B3，A3B2交于C3。且C1,C2,C3共线。

由射影几何中的 对偶原理（此处体现为点线互换）可知，它与帕普斯(Pappus)定理是等价的。

该对偶命题是 布利安桑定理的特例。

明显的，当二次曲线上的 帕斯卡定理中二次曲线退化为两条相交直线（在 射影平面中，我们认为平行直线相交于无穷远点），即为帕普斯(Pappus)定理。