- 最速降线问题

最速降线问题
简介
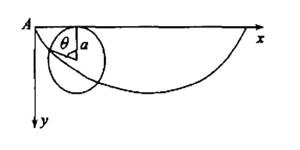 旋轮线在一个斜面上,摆两条轨道,一条是直线,一条是曲线,起点高度以及终点高度都相同。两个质量、大小一样的小球同时从起点向下滑落,曲线的小球反而先到终点。这是由于曲线轨道上的小球先达到最高速度,所以先到达。然而,两点之间的直线只有一条,曲线却有无数条,那么,哪一条才是最快的呢?伽利略与1630年提出了这个问题,当时他认为这条线应该是一条弧线,可是后来人们发现这个答案是错误的。[1]1696年,瑞士数学家约翰·伯努利解决了这个问题,他还拿这个问题向其他数学家提出了公开挑战。牛顿、莱布尼兹、洛比达以及雅克布·伯努利等解决了这个问题。这条最速降线就是一条摆线,也叫旋轮线(连接两个点上凹的唯一一段旋轮线)。
旋轮线在一个斜面上,摆两条轨道,一条是直线,一条是曲线,起点高度以及终点高度都相同。两个质量、大小一样的小球同时从起点向下滑落,曲线的小球反而先到终点。这是由于曲线轨道上的小球先达到最高速度,所以先到达。然而,两点之间的直线只有一条,曲线却有无数条,那么,哪一条才是最快的呢?伽利略与1630年提出了这个问题,当时他认为这条线应该是一条弧线,可是后来人们发现这个答案是错误的。[1]1696年,瑞士数学家约翰·伯努利解决了这个问题,他还拿这个问题向其他数学家提出了公开挑战。牛顿、莱布尼兹、洛比达以及雅克布·伯努利等解决了这个问题。这条最速降线就是一条摆线,也叫旋轮线(连接两个点上凹的唯一一段旋轮线)。
旋轮线与1673年荷兰科学家惠更斯讨论的摆线相同。因为钟表摆锤作一次完全摆动所用的时间相等,所以摆线(旋轮线)又称等时曲线。
看一个稍微有点振奋人心的东西,Johann Bernoulli 对最速降线问题的beautiful解答:
如果使分成的层数n无限地增加,即每层的厚度无限地变薄,则质点的运动便趋于空间A、B两点间质点运动的真实情况,此时折线也就无限增多,其形状就趋近我们所要求的曲线——最速降线.而折线的每一段趋向于曲线的切线,因而得出最速降线的一个重要性质:任意一点上切线和铅垂线所成的角度的正弦与该点落下的高度的平方根的比是常数.而具有这种性质的曲线就是摆线.所谓摆线,它是一个圆沿着一条直线滚动正(无滑动)时,圆周上任意一点的轨迹。
因此,最速降线就是摆线,只不过在最速降线问题中,这条摆线是上、下颠倒过来的罢了.
证明
列出表达式
设O,A是高度
不同,且不在同一铅垂线上的两定点,y
如果不计摩擦和空气阻力,一质点m
在重力作用下从O点沿一曲线降落至 。A(p,q)A点,问曲线呈何种形状时,质点降y
落的时间最短。
图 7-1 设曲线为y=y(x) ,坐标如图 7-1,质点由O点开始运动,它的速度v与它的纵坐标有关系
![]()
式中,g是重力加速度。
在曲线上点 (x,y) 处,质点的运动速度为
![]()
式中,s表示曲线的弧长,t表示时间,于是
![]()
由于点O,A的横坐标分别是 0,p,则质点m从O点运动到A点所需时间为
![]()
(7.1.4)
这样,质点由O点运动到A点所需时间t是y(x)的函数,最速降线问题就是满足边界条件的![]() 所有连续函数y(x)中,求出一个函数y使泛函式(7.1.4)取最小值。
所有连续函数y(x)中,求出一个函数y使泛函式(7.1.4)取最小值。
对泛函求极值的问题称为变分问题,使泛函取极值的函数称为变分问题的解,也称为极值函数。
在微分学中,求函数y=y(x) 的极值是求自变量x的值,当x取这些值时,y取极 大(小)值、取极值的必要条件是dy/dx= 0 。下面我们仿照函数微分的概念来定义泛函的变分概念,进而导出泛函极值存在的必要条件。设y,y0是集合C的元素,称δy=y−y0为函数y在y0处的变分。
这里的δy是x的函数,它与 ∆y的区别在于:变分 δy反映的是整个函数的改变,
而 ∆y表示的是同一个函数y(x)因x的不同值而产生的差异。在本书,我们总是假定y(x)和F(x,y,y′) 都是充分光滑的,且y(x)在两个端点处固定,即
![]()
(7.1.5)
式中,y1,y2是两个常数。
考虑泛函
![]()
(7.1.6)
当函数y(x)有微小改变且变为y(x) +δy(x) 时,利用
![]()
上式可推出
![]()
上式称为J(y)的变分,记为δJ(y),即
![]()
(7.1.7)
下面我们证明,泛函J(y)取极值的必要条件是
![]() (7.1.8)
(7.1.8)
或者
![]()
(7.1.9)
设y=y(x) 使泛函J(y)取极值,取函数y(x)变分的特殊形式为
![]()
式中, ε是任意小的实数;ϕ(x)是充分光滑的任意函数,并且满足条件
![]()
这样,函数
y(x) +εϕ(x) 满足边界条件式(7.1.5)。因此,泛函J[y(x) +εϕ(x)]
当 ε= 0时取最小值J[y(x)] ,从而有
![]()
由于
![]() 则有
则有
![]()
(7.1.10)
则有
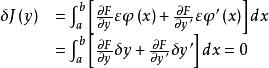
应用分部积分,我们作进一步的分析,有
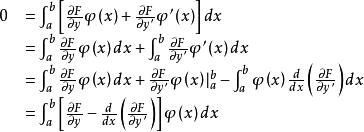
由ϕ(x)的任意性,可得
![]()
(7.1.11)
式(7.1.11)称为欧拉-拉格朗日方程,简记为 E-L方程,
必要条件
y=y(x) 使泛函式(7.1.6)取极小值,则y=y(x) 一定使欧拉-拉格朗日方程式(7.1.11)满足边界条件式(7.1.5)的解。
我们把满足 E-L方程边值问题的解称为驻留函数,对应的积分曲线称为驻留曲线。严格地讲,E-L方程边值问题的解满足变分问题的必要条件,因此它是否是极值函数,还需作进一步的判别。在实际问题中,极值的存在性通常给出问题时已经肯定了,这样,当一个实际现象已知其有唯一的极值存在,而这时也只得到一个驻留函数,则可以判定这个驻留函数就是极值函数。
最终解答
解
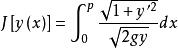
且y(0)=0,y(p)=q
这样
![]()
(7.1.12)
其E-L方程为
![]()
由于
![]()
所以有
![]()
(7.1.13)
将(7.1.12)代入式(7.1.13)
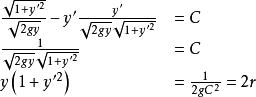
(7.1.14)
引入变量代换x=x(θ),并设y'=cot(θ/2)
则由式(7.1.14)可得
![]()
上式对θ求导,得

所以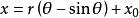
根据曲线过原点(0,0)及(p,q)可求出x0=0及r,这样,所求曲线为[2]
![]()



 求购
求购




