- 拉格朗日中值定理

拉格朗日中值定理
定律定义
定理表述
如果函数f(x)满足:
(1)在闭区间[a,b]上连续;
(2)在开区间(a,b)内可导;
那么在开区间(a,b)内至少有一点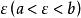 使等式
使等式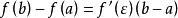 成立。
成立。
其他形式
记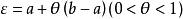 ,令
,令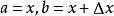 ,则有
,则有
![]()
上式称为有限增量公式。[3]
我们知道函数的微分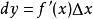 是函数的增量Δy的近似表达式,一般情况下只有当|Δx|很小的时候,dy和Δy之间的近似度才会提高;而有限增量公式却给出了当自变量x取得有限增量Δx(|Δx|不一定很小)时,函数增量Δy的准确表达式,这就是该公式的价值所在。
是函数的增量Δy的近似表达式,一般情况下只有当|Δx|很小的时候,dy和Δy之间的近似度才会提高;而有限增量公式却给出了当自变量x取得有限增量Δx(|Δx|不一定很小)时,函数增量Δy的准确表达式,这就是该公式的价值所在。
验证推导
辅助函数法:
已知![]() 在
在![]() 上连续,在开区间
上连续,在开区间![]() 内可导,
内可导,
构造辅助函数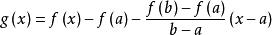
可得g(a)=g(b)又因为![]() 在
在![]() 上连续,在开区间
上连续,在开区间![]() 内可导,
内可导,
所以根据罗尔定理可得必有一点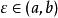 使得
使得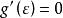
由此可得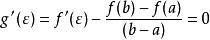
变形得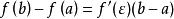
定理证毕。
定理推广
推论
如果函数![]() 在区间
在区间![]() 上的导数
上的导数![]() 恒为零,那么函数
恒为零,那么函数![]() 在区间
在区间![]() 上是一个常数。
上是一个常数。
证明
在区间![]() 上任取两点
上任取两点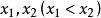 由拉格朗日中值定理得
由拉格朗日中值定理得
![]()
由于已知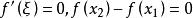 即
即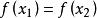
因为![]() 是区间
是区间![]() 上的任意两点,所以
上的任意两点,所以![]() 在区间
在区间![]() 上的函数值总是相等的,
上的函数值总是相等的,
即函数在区间上是一个常数。
推广
如果函数![]() 在开区间
在开区间![]() 内可导且
内可导且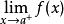 与
与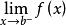 都存在
都存在
令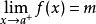 ,
,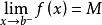
则在开区间![]() 内至少存在一点
内至少存在一点![]() 使得
使得
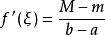
有限增量公式的θ
拉格朗日中值定理有一个变形,即所谓的有限增量公式:f(x0+Δx)-f(x0)=f'(x0+θΔx)Δx,0<θ<1。其中的![]() 有一个很重要的性质:
有一个很重要的性质:
若![]() 在
在![]() 点连续,且
点连续,且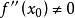 ,则
,则
![]()
证明由于f''(x)在![]() 点连续,所以有
点连续,所以有
(1)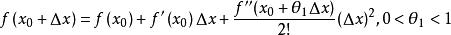 ;
;
(2)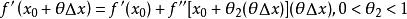 。
。
将(1)和(2)同时代入有限增量公式,可得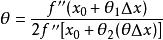 ,,利用f"(x)在x0点处的连续性及f"(x0)≠0,在等式两边同取极限(令
,,利用f"(x)在x0点处的连续性及f"(x0)≠0,在等式两边同取极限(令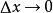 ),即可得结论。
),即可得结论。
导函数连续定理
证明导函数连续定理:
若函数f(x)在x0的某邻域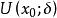 内连续,在
内连续,在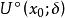 内可导,且
内可导,且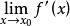 存在,则f(x)在x0处可导,并且有
存在,则f(x)在x0处可导,并且有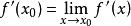 。
。
解析:该定理给出了导函数连续的一个充分条件。(注意:必要性不成立,即函数在某点可导,不能推出导函数在该点连续,因为该点还可能是导函数的振荡间断点。)我们知道,函数在某一点的极限不一定等于该点处的函数值;但如果这个函数是某个函数的导函数,则只要这个函数在某点有极限,那么这个极限就等于函数在该点的取值。
证明:由导数的定义可知,函数在某点可导的充要条件是函数在该点的左右导数相等,因此分别来研究左右导数。
右导数:任取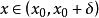 ,显然
,显然![]() 在区间
在区间![]() 上满足定理使用条件。
上满足定理使用条件。
∴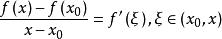
当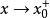 时,有
时,有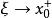 ,对上式两边取极限,得:
,对上式两边取极限,得:
![]()
即:
![]()
上式左边是![]() 在
在![]() 处的右导数,右边是导函数
处的右导数,右边是导函数![]() 在
在![]() 处的右极限。
处的右极限。
同理,有![]()
上式左边是![]() 在
在![]() 处的左导数,右边是导函数
处的左导数,右边是导函数![]() 在
在![]() 处的左极限。
处的左极限。
∵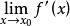 存在
存在
∴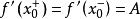
∴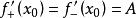
∴f(x)在x0处可导,并且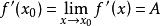
由该定理立即可得出一个推论:如果函数在某个区间上可导,那么导函数在该区间上不存在第一类间断点。换句话说,如果一个函数在某个区间上存在第一类间断点,那么它在该区间上没有原函数。
发展简史
人们对拉格朗日中值定理的认识可以上溯到公元前古希腊时代。古希腊数学家在几何研究中得到如下结论:“过抛物线弓形的顶点的切线必平行于抛物线弓形的底”。这正是拉格朗日定理的特殊情况,古希腊数学家阿基米德正是巧妙地利用这一结论,求出抛物弓形的面积.。
意大利卡瓦列里在《不可分量几何学》(1635年)的卷一中给出处理平面和立体图形切线的有趣引理,其中引理3基于几何的观点也叙述了同样一个事实:曲线段上必有一点的切线平行于曲线的弦。这是几何形式的微分中值定理,被人们称为卡瓦列里定理。该定理是拉格朗日中值定理在几何学中的表达形式。
1797年,法国数学家拉格朗日在《解析函数论》一书中首先给出了拉格朗日定理,他给出的定理的最初形式是:“函数![]() 在
在![]() 与
与![]() 之间连续,
之间连续,![]() 在
在![]() 与
与![]() 之间有最小值
之间有最小值![]() 与最大值
与最大值![]() ,则
,则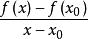 必取
必取![]() 与
与![]() 之间的一个值。”拉格朗日给出最初的证明,但证明并不严格,他给的条件比现在的条件要强,他要求函数
之间的一个值。”拉格朗日给出最初的证明,但证明并不严格,他给的条件比现在的条件要强,他要求函数![]() 在闭区间上具有连续导数
在闭区间上具有连续导数![]() ,并且他所用的连续也是直观的,而不是抽象的。
,并且他所用的连续也是直观的,而不是抽象的。
十九世纪初,在微积分严格化运动中,柯西给出了拉格朗日中值定理的严格证明,在《无穷小计算教程概论》中,柯西证明了”如果导数![]() 在闭区间
在闭区间![]() 上连续,则必存在一点
上连续,则必存在一点![]() ,使得
,使得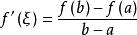 。 ”柯西又在《微分计算教程》中将拉格朗日中值定理推广为柯西中值定理。
。 ”柯西又在《微分计算教程》中将拉格朗日中值定理推广为柯西中值定理。
现代形式的拉格朗日中值定理是由法国数学家博(O.Bonnet)给出的,他不是利用导数![]() 的连续性,而是利用罗尔定理对拉格朗日中值定理进行了重新证明。
的连续性,而是利用罗尔定理对拉格朗日中值定理进行了重新证明。
意义
拉格朗日中值定理是微分中值定理的核心,其他中值定理是拉格朗日中值定理的特殊情况和推广,它是微分学应用的桥梁,在理论和实际中具有极高的研究价值。
几何意义
若连续曲线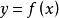 在
在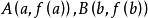 两点间的每一点处都有不垂直于x轴的切线,则曲线在A,B间至少存在1点
两点间的每一点处都有不垂直于x轴的切线,则曲线在A,B间至少存在1点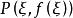 ,使得该曲线在P点的切线与割线AB平行。
,使得该曲线在P点的切线与割线AB平行。
运动学意义
对于曲线运动在任意一个运动过程中至少存在一个位置(或一个时刻)的瞬时速率等于这个过程中的平均速率。
拉格朗日中值定理在柯西的微积分理论系统中占有重要的地位。可利用拉格朗日中值定理对洛必达法则进行严格的证明,并研究泰勒公式的余项。从柯西起,微分中值定理就成为研究函数的重要工具和微分学的重要组成部分。[4]
拉格朗日
法国数学家。1754年开始研究数学,1766年接替了欧拉在柏林皇家科学院的职位,在那里工作达20年。1786年去法国,先后担任巴黎高等师范学校和多科工艺学校教授。他是18世纪仅次于欧拉的大数学家,工作涉及数论、代数方程论、微积分、微分方程、变分法、力学、天文学等许多领域。在数学上,他最早的重要贡献是1859年解决了等周问题,从而开创了变分问题分析形式的一般解法。1766~1787年是他科学研究的多产时期,1766~1773年,他在数论方面做了一系列研究,1766年证明了所谓佩尔(Pell)方程(x-Ay=1)的解的存在性,1770年证明费马的著名命题,每个正整数可表为至多4个平方数之和;1771年证明了著名的所谓威尔逊 (Wilson) 定理; 1773年关于整数的型表示问题获得关键性成果。1767~1777年,他又系统地研究了代数方程论,引入对称多项式理论,置换理论及预解式概念,指出根的排列理论是整个问题的真谛,对后来伽罗华的工作产生了重要影响。在这期间,他还在微积分、微分方程、力学、天文学领域广泛开展研究,导致了他的两部不朽巨著 《分析力学》 (1788)、《微分原理中的解析函数论》(1797)。著名的拉格朗日中值定理、拉格朗日余项、拉格朗日方程,对黎卡提方程的重要研究,对线性微分方程组的研究,对奇解与通解的联系的系统研究,都是这一时期的工作。他也是最先试图为微积分提供严格基础的数学家之一,这使他成为实变函数论的先驱。他还以在数学上追求简明与严格而被誉为第1个真正的分析学家。拿破仑曾评价说:“拉格朗日是数学科学方面高耸的金字塔。”

-
索博尔奇-索特马尔-贝拉格州
2025-08-13 01:42:54 查看详情


 求购
求购







