- 根心定理

根心定理
定义
点对圆的幂
平面上任意一点对圆的幂定义为以下函数:
考虑到圆的方程也可以写为圆心-半径的形式:
由此也可以把点对圆的幂定义为:
这里是点到圆心的距离,是圆的半径。
点对圆的幂的几何意义是明显的:
若点在圆外,则幂为点到圆的切线长度的平方;
若点在圆上,则幂为0;
若点在圆内,则幂为负数,其绝对值等于过点且垂直于的弦长的一半的平方。
根轴
平面上两不同心的圆
显然,对两圆等幂的点集是直线:
该直线称为两圆的根轴。根轴必垂直于两圆的连心线。
若两圆相交,则根轴就是连接二公共点的直线;
若两圆相切,则根轴就是过切点的公切线;
若两圆相离或内含,则根轴完全位于两圆之外,但仍垂直于两圆的连心线。
当圆1和圆2相离或内含时,用尺规作出这两圆的根轴需要依赖“根心定理”(见第三部分)。具体的做法是:另作一个适当的圆3与前两圆都相交,圆3分别与前两圆形成根轴,这两条根轴的交点即是圆1、圆2和圆3的根心,它必定在圆1和圆2所形成的根轴上;同理,再找一个适当的圆4,找到圆1、圆2和圆4的根心。连接所找到的两个根心,即得到圆1和圆2的根轴。
区别
根心与根心定理(解析几何证法)
三个两两不同心的圆
任意两圆形成一条根轴,因而共有三条根轴:
这三条根轴的直线方程(以下简称为根轴方程)是线性相关的,即由其中两个根轴方程进行线性组合,可以得出第三个根轴方程。因此:
(i)若平面上某一点是其中两个根轴方程的公共解(亦即两根轴的公共点),则必定也是第三条根轴上的点。
(ii)若某两个根轴方程无公共解(即平行),则三个根轴方程中的任意两个均无公共解(即三条根轴两两平行)。
具体而言,三个两两不同心的圆的根轴,仅仅包含下面三种情况:
(1)三根轴两两平行;
(2)三根轴完全重合;
(3)三根轴两两相交,此时三根轴必汇于一点,该点称为三圆的根心。
上面所证明的即是“根心定理”。
以上用解析几何的方法证明了根心定理。在平面上,二元方程对应一条曲线,而方程组的解对应着曲线的公共点。利用这个思想,从根轴方程的线性相关性出发,容易得到平面几何上的根心定理。这种证明方法十分简单。
相关例题
以下例题选自2013年(第54届)国际数学奥林匹克竞赛(IMO)第二天第4题:
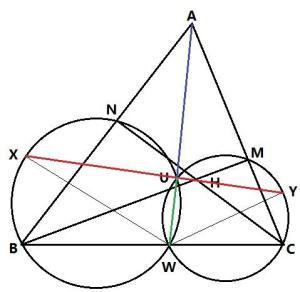
是锐角三角形,H是垂心。W是BC上一点(在B和C之间)。M 和N 分别是从B和C作出的高的垂足。和的外接圆分别记为和。X,Y分别是和上的点,且WX和WY分别是和的直径。
求证: X,Y,H 三点共线。
证明:如图,记和的另一个交点为U,则UW是和的根轴。显然,由于XW和YW分别是两圆的直径,因此XU⊥UW,YU⊥UW,从而X,U,Y共线。
显然,B,C,M,N共圆,记该圆为。注意到BN是和的根轴,而CM是和的根轴。BN和CM交于A点,由根心定理,和的根轴UW必然通过A点,这也就是说A,U,W共线,从而AU⊥XY。
记的外接圆为。显然,由于AN⊥NH,AM⊥MH,因此A,M,H,N四点共圆,即H也在上。
由密克定理,可以直接证明U也在上(从而U就是、和的公共点),从而A,N,U,H,M五点共圆,AH是该圆的直径,则必有AU⊥UH,再由A,U,W共线,知UH⊥UW,从而X,U,H,Y四点共线。
证毕。
注:Miquel定理的内容如下:在△ABC的BC,AC,AB边上分别取点W,M,N,对△AMN,△BWN和△CWM分别作其外接圆,则这三个外接圆共点,且该公共点是这三个圆的根心。
该定理的证明很简单,利用“圆内接四边形对角和为180度”及其逆定理。现在已知U是和的公共点。连接UM和UN,则四边形BNUW和四边形CMUW分别是和的内接四边形,∠UWB+∠UNB=∠UNB+∠UNA=180度,从而∠UWB=∠UNA。同理∠UWB+∠UWC=∠UWC+∠UMC=180度,从而∠UWB=∠UMC。又有∠UMC+∠UMA=180度,因此∠UNA+∠UMA=180度,这正说明四边形ANUM是一个圆内接四边形,而该圆必是,U必在上。



 求购
求购







