- 极化恒等式

极化恒等式
定义
当![]() 是内积空间,
是内积空间,![]() 是由内积所导出的范数时,内积也可以用范数来表达。当
是由内积所导出的范数时,内积也可以用范数来表达。当![]() 是实内积空间时
是实内积空间时
![]() 当
当![]() 是复内积空间时
是复内积空间时
![]() 这两个等式可以直接从内积的定义导出。等式(1)和(2)称为极化恒等式[2]。
这两个等式可以直接从内积的定义导出。等式(1)和(2)称为极化恒等式[2]。
相关定理
Aldaz(2009)给出了如下有意义的结果[2]。
定理1
设![]() 是复内积空间,对任意非零向量
是复内积空间,对任意非零向量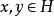 ,有
,有
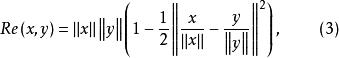
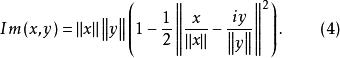 特别地,当
特别地,当![]() 是实内积空间时,
是实内积空间时,
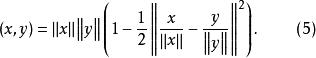 证明:由极化恒等式(2)得到
证明:由极化恒等式(2)得到
![]()
![]() 以
以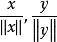 分别代替
分别代替![]() 和
和![]() ,并展开右端第一项即可得到式(3)和式(4),式(5)的证明是类似的。证毕。
,并展开右端第一项即可得到式(3)和式(4),式(5)的证明是类似的。证毕。
在定理1条件下,成立恒等关系
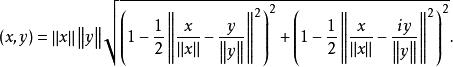
定理2
设![]() 是复内积空间,对任意非零向量
是复内积空间,对任意非零向量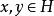 ,有
,有
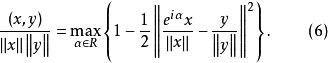
证明:不妨假设![]() 是单位向量,由式(3)知,
是单位向量,由式(3)知,
![]() 等号成立当且仅当存在
等号成立当且仅当存在![]() 使得
使得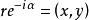 ,证毕[2]。
,证毕[2]。
由式(6)容易得到GBS不等式。

相关百科
-
电容储能型分布式极化率仪系统
2025-09-22 04:17:27 查看详情


 求购
求购









