- 拿破仑定理
拿破仑定理
定理定义
拿破仑定理：
向任何三角形三边分别向外侧作等边三角形，然后把这三个正三角形的中心连结起来所构成的三角形一定是等边三角形。
这一定理可以等价描述为：若以任意三角形的各边为底边向形外作底角为60°的等腰三角形，则它们的中心构成一个等边三角形。
验证推导
在△ABC的各边上向外各作等边△ABF，等边△ACD，等边△BCE。 如何证明：这3个等边三角形的外接圆共点？ 思路：利用四点共圆来证明三圆共点。这是证明拿破仑定理的基础。 证明：设等边△ABF的外接圆和等边△ACD的外接圆相交于O；连接AO、CO、BO。 ∴ ∠AFB=∠ADC=60°； ∵ A、F、B、O四点共圆；A、D、C、O四点共圆； ∴ ∠AOB=∠AOC=120°； ∴ ∠BOC=120°； ∵ △BCE是等边三角形 ∴ ∠BEC=60°； ∴ B、E、C、O四点共圆； ∴ 这3个等边三角形的外接圆共点。 结论：因为周角等于360°，所以，∠AOB=∠AOC=120°时，∠BOC就等于120°；用四点共圆的性质定理和判定定理来证明三圆共点的问题 |
|
以任意三角形的三边为边向外作等边三角形，则这三个等边三角形的中心的连线是一个等边三角形。 求证：上面3个等边三角形的中心M、N、P的连线构成一个等边三角形？ 思路：利用已有的三个圆和三个四点共圆来证明。 证明：设等边△ABD的外接圆⊙N，等边△ACF的外接圆⊙M，等边△BCE的外接圆⊙P 相交于O；连AO、CO、BO。 ∵ A、D、B、O四点共圆； A、F、C、O四点共圆 B、E、C、O四点共圆 ∠AFC=∠ADB=∠BEC=60°； ∴ ∠AOB=∠AOC=∠BOC=120°； ∵ NP、MP、MN是连心线； BO、CO、AO是公共弦； ∴ BO⊥NP于X； CO⊥MP于Y； AO⊥NM于Z。 ∴ X、P、Y、O四点共圆； Y、M、Z、O四点共圆； Z、N、X、O四点共圆； ∴ ∠N=∠M=∠P=60°； 即△MNP是等边三角形。[1] |
 |
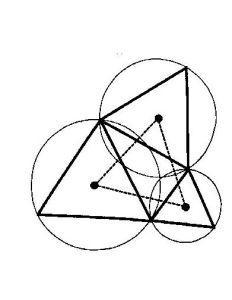
费马点也是证明拿破仑定理的好方法。
右图即是用费马点的性质来推导拿破仑定理的证明方法。
推广拓展
在△ABC的各边上向外各作等边△ABF，等边△ACD，等边△BCE。 如何证明：这3个等边三角形的外接圆共点？ 思路：利用四点共圆来证明三圆共点。这是证明拿破仑定理的基础。 证明：设等边△ABF的外接圆和等边△ACD的外接圆相交于O；连接AO、CO、BO。 ∴ ∠AFB=∠ADC=60°； ∵ A、F、B、O四点共圆；A、D、C、O四点共圆； ∴ ∠AOB=∠AOC=120°； ∴ ∠BOC=120°； ∵ △BCE是等边三角形 ∴ ∠BEC=60°； ∴ B、E、C、O四点共圆； ∴ 这3个等边三角形的外接圆共点。 结论：因为周角等于360°，所以，∠AOB=∠AOC=120°时，∠BOC就等于120°；用四点共圆的性质定理和判定定理来证明三圆共点的问题 |
|
以任意三角形的三边为边向外作等边三角形，则这三个等边三角形的中心的连线是一个等边三角形。 求证：上面3个等边三角形的中心M、N、P的连线构成一个等边三角形？ 思路：利用已有的三个圆和三个四点共圆来证明。 证明：设等边△ABD的外接圆⊙N，等边△ACF的外接圆⊙M，等边△BCE的外接圆⊙P 相交于O；连AO、CO、BO。 ∵ A、D、B、O四点共圆； A、F、C、O四点共圆 B、E、C、O四点共圆 ∠AFC=∠ADB=∠BEC=60°； ∴ ∠AOB=∠AOC=∠BOC=120°； ∵ NP、MP、MN是连心线； BO、CO、AO是公共弦； ∴ BO⊥NP于X； CO⊥MP于Y； AO⊥NM于Z。 ∴ X、P、Y、O四点共圆； Y、M、Z、O四点共圆； Z、N、X、O四点共圆； ∴ ∠N=∠M=∠P=60°； 即△MNP是等边三角形。[1] |
|
定理历史
四边形上，类似的定理为凡·奥贝尔定理。
拿破仑定理本身为佩特诺-伊曼-道格拉斯定理的特例。
内拿破仑三角形的面积大于等于 0 给出外森比克不等式。
词条图册
拿破仑定理拿破仑为人颇为好学，是法兰西科学院院士，他对数学方面很感兴趣，自幼喜爱数学。他在行军打仗的空闲时间，经常研究平面几何。他对数学和数学家怀有特别的敬意，并且欣赏他自己提出的问题。他在这方面证明了“拿破仑三角形”即拿破仑定理。
求购