

对偶理论



对偶理论

目录导航

简介

　　对偶理论：Duality theory冯·偌依曼

研究线性规划中原始问题与对偶问题之间关系的理论。

　　对偶理论属自动控制与系统工程范畴

　　对偶理论主要研究经济学中的相互确定关系，涉及到经济学的诸多方面。产出与成本的对偶、效用与支出的对偶，是经济学中典型的对偶关系。经济系统中还有许多其他这样的对偶关系。

　　利用对偶性来进行经济分析的这种方法，就叫做对偶方法。

　　每一个线性规划问题都存在一个与其对偶的问题，在求出一个问题解的同时，也给出了另一个问题的解。

　　对偶理论，1947年由美籍匈牙利数学家冯·偌依曼提出创立。

发展简史

　　在线性规划早期发展中最重要的发现就是对偶问题，即每一个线性规划问题(称为原始问题)都有一个与它对应的对偶线性规划问题（称为对偶问题）。1928年美籍匈牙利数学家冯·诺伊曼在研究对策论时已发现线性规划与对策论之间存在着密切的联系。两人零和对策可表达成线性规划的原始问题和对偶问题。他于1947年提出对偶理论。1951年G.B.丹齐克引用对偶理论求解线性规划的运输问题，研究出确定检验数的位势法原理。1954年C.莱姆基提出对偶单纯形法，成为管理决策中进行灵敏度分析的重要工具。对偶理论有许多重要应用：在原始的和对偶的两个线性规划中求解任何一个规划时，会自动地给出另一个规划的最优解；当对偶问题比原始问题有较少约束时，求解对偶规划比求解原始规划要方便得多；对偶规划中的变量就是影子价格。相关书籍

　　对偶问题，每一个线性规划问题都伴随有另一个线性规划问题，称为对偶问题。原来的线性规划问题则称为原始线性规划问题，简称原始问题。对偶问题有许多重要的特征，它的变量能提供关于原始问题最优解的许多重要资料，有助于原始问题的求解和分析。对偶问题与原始问题之间存在着下列关系：①目标函数对原始问题是极大化，对对偶问题则是极小化。②原始问题目标函数中的收益系数是对偶问题约束不等式中的右端常数，而原始问题约束不等式中的右端常数则是对偶问题中目标函数的收益系数。③原始问题和对偶问题的约束不等式的符号方向相反。④原始问题约束不等式系数矩阵转置后即为对偶问题的约束不等式的系数矩阵。⑤原始问题的约束方程数对应于对偶问题的变量数，而原始问题的变量数对应于对偶问题的约束方程数。⑥对偶问题的对偶问题是原始问题，这一性质被称为原始和对偶问题的对称性。

基本定理

　　原始问题和对偶问题的标准形式如下：

　　原始问题　对偶问题

　　max　z＝cx　min　w＝yb

　　s.t.　Ax≤b　s.t.　yA≥c

　　x≥0　y≥0

　　式中max表示求极大值,min表示求极小值,s.t.表示“约束条件为”；z为原始问题的目标函数，w为对偶问题的目标函数；x为原始问题的决策变量列向量（n×1），y为对偶问题的决策变量行向量(1×m);A为原始问题的系数矩阵(m×n),b为原始问题的右端常数列向量（m×1），c为原始问题的目标函数系数行向量（1×n）。在原始问题与对偶问题之间存在着一系列深刻的关系，业已得到严格数学证明的有如下一些定理。

弱对偶定理

　　若上述原始问题和对偶问题分别有可行解x0和y0,则y0b≥cx0。这个定理表明极大化问题任一可行解的目标函数值总是不大于它的对偶问题的任一可行解的目标函数值。　

　　强对偶定理若上述原始问题和对偶问题都可行，则它们分别有最优解x*和y*，且cx*=y*b。

最优准则定理

　　若上述原始问题和对偶问题分别有可行解x0和y0,且两者的目标函数值相等，即y0b=cx0,则两个可行解分别为对应线性规划的最优解。

互补松弛定理

　　若上述原始问题和对偶问题分别有可行解x0和y0，且u0和v0分别为它们的松弛变量,则当且仅当v0x0+u0y0时，x0和y0分别为它们的最优解。

松弛定理

　　若上述原始问题和对偶问题分别有可行解x0和y0,且u0和v0分别为它们的松弛变量，则当且仅当v0x0=0和u0y0=0时, x0和y0分别为它们的最优解。v0x0=0和u0y0=0这两个等式称为互补松弛条件。　

　　对称对偶线性规划具有对称形式的线性规划的特点是：

　　①全部约束条件均为不等式，对极大化问题为≤，对极小化问题为≥。

　　②全部变量均为非负。

　　列出对称对偶线性规划的步骤是：

　　①规定非负的对偶变量，变量数等于原始问题的约束方程数。

　　②把原始问题的目标函数系数作为对偶问题约束不等式的右端常数。

　　③把原始问题约束不等式的右端常数作为对偶问题的目标函数系数。

　　④把原始问题的系数矩阵转置后作为对偶问题的系数矩阵。

　　⑤把原始问题约束条件中的不等号反向作为对偶问题约束条件的不等号。

　　⑥将原始问题目标函数取极大化改成对偶问题目标函数取极小化。　

　　非对称对偶线性规划有时线性规划并不以对称方式出现，如约束条件并不都是同向不等式，变量可以是非正的或没有符号约束。

　　列写非对称对偶线性规划可参照原始-对偶表（见表）按下列步骤进行：

　　①规定对偶变量，变量个数等于原始问题约束不等式数。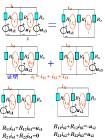对偶理论

　　②把原始问题的目标函数系数作为对偶问题约束不等式的右端常数。

　　③把原始问题约束不等式的右端常数作为对偶问题的目标函数系数。

　　④把原始问题的系数矩阵转置后作为对偶问题的系数矩阵。

　　⑤根据原始问题的约束不等式情况，确定对偶变量的符号约束。

　　⑥根据原始问题决策变量的符号约束，确定对偶问题约束不等式的符号方向。　

　　对偶问题的最优解从原始问题的最终单纯形表中（最优单纯形算子）可直接得到对偶问题的最优解。原始问题中松弛变量的检验数对应着对偶问题的解（符号相反）。在用单纯形法时每一步迭代可得到原始问题的可行解x0和对偶问题的补充解y0,且cx0=y0b,若x0不是原始问题的最优解，y0就不是对偶问题的可行解。最后一步迭代得到原始问题的最优解x*和对偶问题的补充最优解y*，且cx*=y*b。y*是原始问题的影子价格。

对偶原理

　　在平面几何中，点和线称为对偶元素。过一点画一条直线和在一条直线上标出一个点叫作对偶运算。两个图形，如果一个可以从另一个把其中的元素和运算替换为对偶的元素和运算而达到，就称为对偶的。两个定理，如果一个定理中的所有元素和运算替换为对偶的就成为另一个定理时，叫做对偶的。如果其中一个定理真实，则另一个必然真实。关于上述这一事实，是彭色列在建立射影几何学理论时首先发现的。事实上，射影几何中所有的定理都是成对出现的。于是我们在射影几何内有如下对偶原理：

　　射影几何中的任一个成立的定理的对偶，同样是射影几何中的一个真实的定理。

　　是什么保证了这个对偶原理的正确性呢？这要追溯到几何基础的公理系统中去。在希尔伯特几何公理系统中的点、线、面、位于、通过等名词都是一些抽象的元素和关系，可以允许给予不同的具体解释。其演绎系统的性质，完全由公理系统中成立的关系给出。我们可以把射影几何也建立在这样的抽象元素和关系的公理系统上去。我们给出无定义的点、线和关联，以及象下面这样的对偶公理：“每两个不同的点关联着唯一的一条直线”和“每两条不同的直线关联着唯一的一点”等等。这样一来，任何一个定理，如果在它的叙述和证明中，只包含与对偶公理有关的元素，那么其中一定准许对偶化。因为原定理的证明在于某些公理的连续应用，而按同样顺序应用其对偶原理，这样就得到了关于对偶定理的证明。正由于公理的对偶性，才保证了对偶原理的正确性。

　　对偶是一种广义对称。对称是数学美的重要特征之一。因此，对偶原理从方法论的角度来讲，便是数学的美学方法的一个具体体现，而且这一美学方法又与真紧密联系在一起，因此，它的作用也就显得更加重要了。