切线长定理

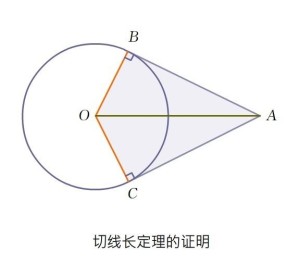定理证明示意图以下简述切线长定理的证明。

欲证AC=AB，只需证△ABO≌ △ACO。

如图，OC、OB为圆的两条半径，又∠ABO= ∠ACO=90°

在Rt△ABO和Rt△ACO中

∴Rt△ABO≌ Rt△ACO（H.L）

∴AB=AC，且∠AOB=∠AOC，且∠OAB=∠OAC。^[3]

切线长定理(3)切线长定理推论：

·圆的外切四边形的两组对边的和相等；

·从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

观察、猜想、证明，形成定理

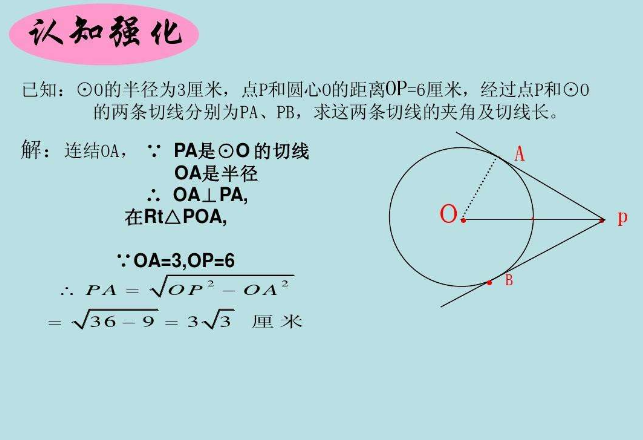
1、切线长的概念． 如图，P是⊙O外一点，PA，PB是⊙O的两条切线，我们把线段PA，PB叫做点P到⊙O的切线长．引导学生理解：切线和切线长是两个不同的概念，切线是直线，不能度量；切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量。

2、观察 利用电脑变动点P 的位置，观察图形的特征和各量之间的关系．

3、猜想 引导学生直观判断，猜想图中PA是否等于PB． PA=PB．

4、证明猜想，形成定理． 猜想是否正确。需要证明． 组织学生分析证明方法．关键是作出辅助线OA，OB，要证明PA=PB．

想一想：根据图形，你还可以得到什么结论？ ∠OPA=∠OPB(如图)等．

由此，引导学生推出切线长定理。

5、归纳： 把前面所学的切线的5条性质与切线长定理一起归纳切线的性质

切线的性质：

(1)切线和圆只有一个公共点；

(2)切线和圆心的距离等于圆的半径；

例题(3)切线垂直于经过切点的半径；(4)经过圆心垂直于切线的直线必过切点；

(5)经过切点垂直于切线的直线必过圆心；

6、切线长定理的基本图形研究

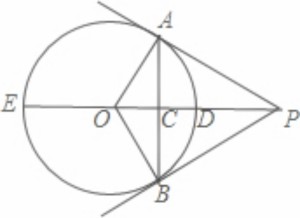
例如这道：如图，PA，PB是⊙O的两条切线，A，B为切点．直线OP交⊙O于点D，E，交AB于C

(1)写出图中所有的垂直关系； (2)写出图中所有的全等三角形； (3)写出图中所有的相似三角形； (4)写出图中所有的等腰三角形．

说明：对基本图形的深刻研究和认识是在学习几何中关键，它是灵活应用知识的基础。

如右图，AB、AC与⊙O相切，连接BC，设BC与AO交于点H。

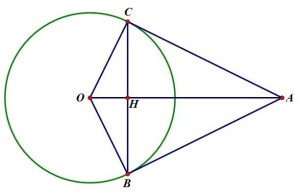
求证：AO⊥BC

∵AB、AC与⊙O相切

∴∠ABO=∠ACO=90°

在Rt△ABO和Rt△ACO中

∠ABO=∠ACO=90°

BO=CO

AO=AO

∴RtΔABO≌RtΔACO（HL）

∴∠AOB=∠AOC

在△BOH和△COH

∠AOB=∠AOC

BO=CO

OH=OH

∴△BOH≌△COH（S.A.S)

∴∠BHO=∠CHO

∵∠BHO+∠CHO=180°

∴∠CHO=∠BHO=90°

∴BC⊥AO。^[4]

（或更简单，∵RtΔABO≌RtΔACO（HL），易得RtΔABO与RtΔACO关于AO轴对称。由轴对称的性质：对称轴垂直平分连接对应点的线段可得，BC⊥AO。）