托勒密定理

托勒密定理一般几何教科书中的“托勒密定理”，实出自 依巴谷(Hipparchus)之手，托勒密只是从他的书中摘出。

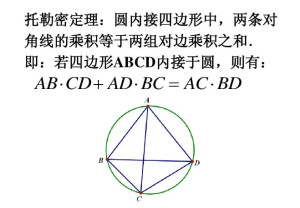
摘出并完善后的托勒密(Ptolemy)定理指出，圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。

定理表述：圆的内接四边形中，两对角线所包矩形的面积等于 一组对边所包矩形的面积与另一组对边所包矩形的面积之和。

从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质．

指圆内接 凸四边形两对对边乘积的和等于两条对 角线的乘积。

一、（以下是推论的证明，托勒密定理可视作特殊情况。）

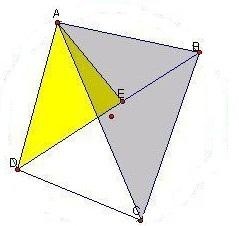
在 任意凸四边形ABCD中(如右图)，作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD,连接DE.

则△ABE∽△ACD

所以 BE/CD=AB/AC,即BE·AC=AB·CD (1)由△ABE∽△ACD得AD/AC=AE/AB,又∠BAC=∠EAD,

所以△ABC∽△AED.

BC/ED=AC/AD,即ED·AC=BC·AD (2)

(1)+(2),得

AC(BE+ED)=AB·CD+AD·BC

又因为BE+ED≥BD

（仅在四边形ABCD是某圆的内接四边形时，等号成立，即“托勒密定理”）

复数证明

用a、b、c、d分别表示四边形顶点A、B、C、D的 复数，则AB、CD、AD、BC、AC、BD的长度分别是：(a-b)、(c-d)、(a-d)、(b-c) 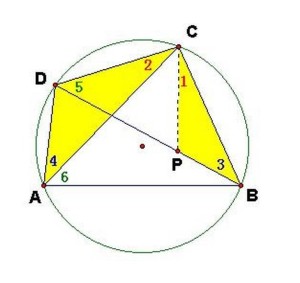托勒密定理、(a-c)、(b-d)。 首先注意到 复数 恒等式： ( a− b)( c− d) + ( a− d)( b− c) = ( a− c)( b− d) ，两边取模，运用 三角不等式得。等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等，这与A、B、C、D四点共 圆等价。 四点不限于同一平面。 平面上，托勒密不等式是三角不等式的 反演形式。

二、

设ABCD是 圆内接四边形。 在弦BC上， 圆周角∠BAC = ∠BDC，而在AB上，∠ADB = ∠ACB。 在AC上取一点K，使得∠ABK = ∠CBD； 因为∠ABK + ∠CBK = ∠ABC = ∠CBD + ∠ABD，所以∠CBK = ∠ABD。 因此△ABK与△DBC相似，同理也有△ABD ~ △KBC。 因此AK/AB = CD/BD，且CK/BC = DA/BD； 因此AK·BD = AB·CD，且CK·BD = BC·DA； 两式相加，得(AK+CK)·BD = AB·CD + BC·DA； 但AK+CK = AC，因此AC·BD = AB·CD + BC·DA。证毕。

三、

托勒密定理：圆内接 四边形中，两条 对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和)．已知：圆内接四边形ABCD，求证：AC·BD=AB·CD+AD·BC．

证明：如图1，过C作CP交BD于P，使∠1=∠2，又∠3=∠4，∴△ACD∽△BCP．得AC：BC=AD：BP，AC·BP=AD·BC ①。又∠ACB=∠DCP，∠5=∠6，∴△ACB∽△DCP．得AC：CD=AB：DP，AC·DP=AB·CD ②。①+②得 AC(BP+DP)=AB·CD+AD·BC．即AC·BD=AB·CD+AD·BC．

四、广义托勒密定理：设四边形ABCD四边长分别为a,b,c,d,两条对角线长分别为m、n，则有：

m 2*n 2=a 2*c 2+b 2*d 2-2abcd*cos(A+C)

托勒密不等式：凸四边形的两组对边乘积和不小于其对角线的乘积，取等号当且仅当共圆或共线。

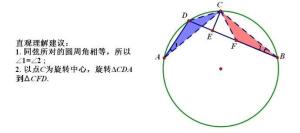托勒密定理  简单的证明：复数恒等式：(a-b)(c-d)+(a-d)(b-c)=(a-c)(b-d)，两边取模，

得不等式AC·BD≤|(a-b)(c-d)|+|(b-c)(a-d)|=AB·CD+BC·AD

1.任意 凸四边形ABCD，必有AC·BD≤AB·CD+AD·BC，当且仅当ABCD 四点共圆时取等号。

2.托勒密定理的 逆定理同样成立：一个凸四边形两对对边乘积的和等于两条对角线的乘积，则这个凸四边形内接于一圆

托勒密定理(3)1.等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等，这与A、B、C、D四点共圆等价。

2.四点不限于同一平面。

欧拉定理：在一条线段上AD上，顺次标有B、C两点，则AD·BC+AB·CD=AC·BD