内蕴性质

给定高斯概率空间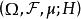，它的数值模型依赖于 H 的基的选取。称其不依赖 H 基选取的性质为内蕴性质，如混沌分解。^[1]

在相对论里， 一个物理观察者，他在自己所处的空间里所能做的几何测量只能是内蕴性质的测量。比如，一个压扁在卷曲的白纸上的小虫，它通过测量可以得出自己所在的空间是欧氏空间，即曲率为零。 但是在三维空间的人看来， 这张白纸是弯曲的。

所谓“内蕴”，是相对于“外嵌”而言。指的是曲面（或曲线）不依赖于它在三维空间中嵌入方式的某些性质。

“内蕴”的概念也可以被解释得更为物理一些：一个观察者在自己生活的物理空间中所能够观察和测量到的几何性质就是这个空间的内蕴性质。也有人比喻说：外嵌是机械设计工程师看待曲面的方法，将曲面看成为他的三维机械零件的表面；而内蕴几何则是地球上的测地员测量地球表面测量到的几何性质。

比如说，内蕴几何量的最简单例子就是弧长。一条直线可以在3维空间中看起来转弯抹角地任意弯曲，即随意改变它的曲率和挠率，但生活在直线上的“点状蚂蚁”观察不到这些“弯来绕去”，只能测量到它爬过的弧长。因此，空间曲线的曲率和挠率，是三维空间的生物观察这条曲线时得到的重要性质，但却并不是内蕴几何量。对曲面来说也是如此，弧长并不因为平面卷成了柱面或锥面而改变。弧长与曲线嵌入空间中的弯曲情况无关，因而是个内蕴几何量。