正五边形

正五边形是指五个边等长且五个角等角的五边形，其内角为108度，是一种正多边形，在施莱夫利符号中可以用来表示。

正五边形的中心角为72度，其具有五个对称轴，其旋转对称性有5个阶（72°、144°、216° 和 288°）。

高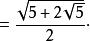边长边长

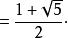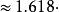宽边长边长

对角线长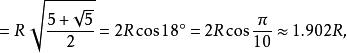

其中R为外接圆半径。

边长为t的正凸五边形面积可以将之分割成5个等腰三角形计算：

正五边形不能镶嵌平面，因为其内角是108°，不能整除360°。截至2015年，已知有15种凸五边形镶嵌平面，还未知道是否尚有其他的凸五边形。

正多边形的面积公式为：

其中，P是周长、r是边心距。正五边形的P和r可由三角函数计算：

其中，t是正五边形的边长。

正五边形是一个圆外切多边形，因此有内切圆。其内切圆半径与边心距相同，并且可以尤其边长来决定。

其中，r为内切圆半径与边心距相同、t为正五边形边长。

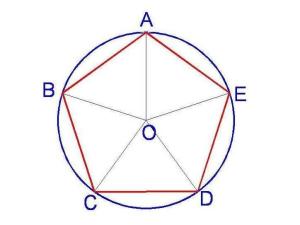正五边形里士满提出了一个构造正五边形的方法，并且在克伦威尔的《多面体》中被近一步讨论。。

先利用单位圆决定五边形的半径。C为单位圆圆心，M是圆C半径的中点。D是位于垂直于MC的另外一条半径的圆周上。作角CMD的角平分线，令Q为角CMD的角平分线与CD的交点。作过Q平行于MC的直线，令之与圆C相交的交点为P，则DP为正五边形的边长。

这条边的长度可以利用圆下方的两个直角三角形DCM和QCM。利用勾股定理，较大的三角形斜边为。小三角形其中一股h可由半角公式求得：

其中，角ϕ可由大三角形求得，其值为：

由此可得到在下图正五边形的边长的一些相关值。右侧三角形的边长a可借由再带一次勾股定理得：

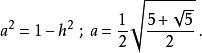欲求出五边形边长s可透过左侧的三角形，由勾股定理得：

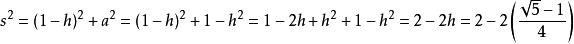
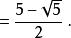使用圆规与直尺建构出正五边形。

五边形边长s为：

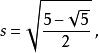得到了正确的结果因此此种构造正五边形的方法是有效的。

约前300年，欧几里得在他的《几何原本》中描述了一个用直尺和圆规做出正五边形的过程。^[2]

正五边形可以借由尝试在一张长条纸张上打一个反手结，并将多出来的部分向后折来构造。这种折法被用在折纸星星上。

(1)已知边长作正五边形的近似画法^[3]

①作线段AB等于定长l，并分别以A,B为圆心，已知长l为半径画弧与AB的中垂线交于K。

②取AB的2/3长度，沿着中垂线向上取C点，使CK=2/3AB。

③以点C为圆心，已知边长AB为半径画弧，分别与前两弧相交于M，N。

④顺次连接A，B，N，C，M各点即近似作得所要求的正五边形。^[4]

(2)民间口诀画正五边形

口诀介绍：“九五顶五九,八五两边分”。

画法:

①画线段AB=20mm。

②作线段AB的垂直平分线l，垂足为G。

③在l上连续截取GH，HD，使 GH=9.5/5*10mm=19mm，HD=5.9/5*10mm=11.8mm。

④过H作EC⊥HG,在EC上截取HE=HC=8/5*10mm=16mm。

⑤连结DE，EA，AB，BC，CD。

五边形ABCDE就是边长为20mm的近似正五边形。

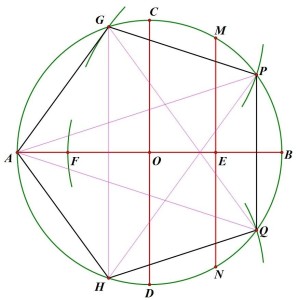图1.正五边形-几何画板理论依据：cos36°=(1+√5)/4

1. 在平面内作一圆，圆心为O；

2. 在圆O上取一点A，连接AO并延长交圆O于另一点B；【假令|AB|=4】

3. 过点O作CD⊥AB，交圆O于C、D两点；【此时|CD|=4】

4. 作OB垂直平分线MN，交OB于E点，交圆O于M，N【此时|OE|=|BE|=1】

5. 以点E为圆心，EC长为半径作弧，交BO延长线于点F；

【此时|EC|=|EF|=√5】

6. 以点B为圆心，BF长为半径作弧，交圆O分别于G、H两点；【此时|BF|=|EF|+|BE|=1+√5】

【此时可知cos∠ABG=(|EF|+|BE|)/|AB|=(1+√5)/4=cos36°】

【而∠AOG=2∠ABG=72°=360°/5(直径所对的圆周角)】

【此时便得到了圆周上的五等分点的其中两个】

7. 以点G为圆心，GA长为半径作弧，交圆O于P点；

8. 以点H为圆心，HA长为半径作弧，交圆O于Q点；

9. 连接AG、GP、PQ、QH、HA,则五边形AGPQH为正五边形。

圆内接正五边形指内接于圆的正五边形。圆内接正五边形的每一条边相等（即圆的每一条弦相等），每个角均为108°，每个角在圆内所对的优弧相等。

因为五边形的内角和可看为3个三角形的内角和，所以，3×180°=540°

据上一条“正五边形的内角和求法”可知道，正五边形的内角和为540°。

往下拓展：因为正五边形的五个角均相等，且五边形的内角和为540°；

所以正五边形的每个内角均为540°÷5=108°