棱柱

定义1：上下底面平行且全等，侧棱平行且相等的封闭几何体叫棱柱。

定义2：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，这些面围成的几何体叫棱柱。

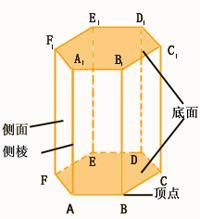棱柱在一个棱柱中：

• 两个相互平行的面叫做棱柱的底面，其余各面叫做棱柱的侧面；
• 两个面的公共边叫做棱柱的棱，其中两个侧面的公共边叫做棱柱的侧棱，侧面与底面的公共顶点叫做棱柱的顶点；
• 不在同一个面上的两个顶点的连线叫做棱柱的对角线；
• 两个底面之间的距离叫做棱柱的高

1. 可以用棱柱的两平行多边形表示棱柱（如棱柱ABCDEF-A1B1C1D1E1F1）。
2. 可以用棱柱的对角线来表示棱柱（如棱柱AD1）。

根据侧棱与底面的关系、底面的形状不同，棱柱可分为斜棱柱、直棱柱和正棱柱。

斜棱柱是侧棱与底面不垂直的棱柱。

直棱柱是侧棱与底面垂直的棱柱。

正棱柱是侧棱与底面垂直且底面为正多边形的棱柱。

根据底面多边形的边数不同，棱柱可分为三棱柱、四棱柱、……、n棱柱。

一些棱柱的特殊名称如下：

• 底面为平行四边形的棱柱叫做平行六面体；
• 侧棱与底面垂直的平行六面体（四棱柱）叫做直平行六面体；
• 长方体和正方体都是直平行六面体；
• 正方体不仅是直平行六面体，也是正棱柱

设棱柱的体积为，底面面积为，底面相对应的高为，则棱柱的体积公式为：

棱柱(3)设n棱柱的表面积为，底面面积为，侧面面积分别为、、……、，则棱柱的表面积公式为：

1. 棱柱的各个侧面都是平行四边形，所有的侧棱都平行且相等；直棱柱的各个侧面都是矩形；正棱柱的各个侧面都是全等的矩形。
2. 棱柱的两个底面与平行于底面的截面是对应边互相平行的全等多边形。
3. 过棱柱不相邻的两条侧棱的截面都是平行四边形。
4. 直棱柱的侧棱长与高相等；直棱柱的侧面及经过不相邻的两条侧棱的截面都是矩形。
5. 棱柱是由一个由直线构成的平面沿着不平行于此平面的直线整体平移而形成的。

展开图是指空间形体的表面在平面上摊平后得到的图形。直棱柱展开图的绘制对于模型和空心工件的制作有重要作用。

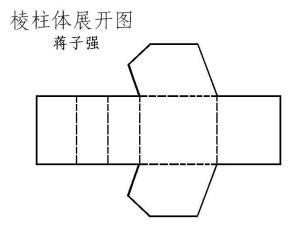如果沿着直棱柱的两个底面和一条棱线将其展开，则会得到右图所示的展开图。从图中不难得出棱柱展开图的特点：

（1）棱柱的所有侧面都是矩形且都有一边相等。

（2）棱柱体两个底面的边展开后形成两条平行且相等的线段，与棱柱所有棱线垂直。

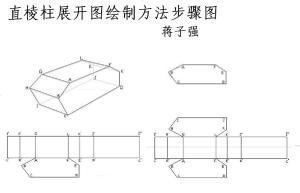根据直棱柱展开图的特点，可以绘制出直棱柱的展开图。

1.找出棱柱体的两个底面，依据透视原理画出它们其中一个的真形。

2.确定棱柱体的高度，过棱柱体底面的最高水平边的端点向上作两条与棱柱体的高度等长的线段。

3.向两边延长棱柱体底面的最高水平边，过两条垂线段的较高端点作一条直线，构成一组平行线。在靠下的直线上依次截取与棱柱体底面各边（底面的最高水平边除外）等长的线段（注意对应关系），得到几个直线上的点，过这些点向上作垂线，交上面的水平直线于几点上。棱柱体的侧面就画好了。

4.将各条垂线段的中点找出，过这些点作一条直线，以这条直线为对称轴作棱柱体底面的轴对称图形。