- 四棱柱

四棱柱
概念
棱柱的底面:棱柱中两个互相平行的面,叫做棱柱的底面。
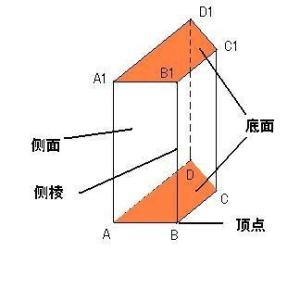 四棱柱四棱柱: 底面为四边形的棱柱是四棱柱。
四棱柱四棱柱: 底面为四边形的棱柱是四棱柱。
斜四棱柱:侧棱不垂直于底面的四棱柱叫做斜四棱柱。
直四棱柱:侧棱垂直于底面的四棱柱叫做直棱柱。
四棱柱有八个顶点、十二条棱、六个面
性质
四棱柱的侧面:四棱柱中除两个底面以外的其余各个面都叫做四棱柱的侧面,四棱柱有4个侧面。[3]
四棱柱的侧棱:四棱柱中两个侧面的公共边叫做棱柱侧棱,四棱柱有4条侧棱。
四棱柱的棱:四棱柱一共有12条棱。侧棱有4条。
1)四棱柱的各个侧面都是平行四边形,所有的侧棱都平行且相等;直四棱柱的各个侧面都是矩形;正四棱柱的各个侧面都是全等的矩形。
2)四棱柱的两个底面与平行于底面的截面是对应边互相平行的全等多边形。
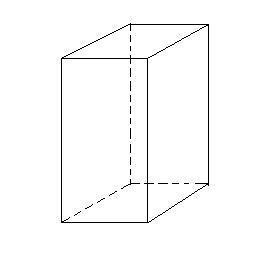 非正四棱柱3)过四棱柱不相邻的两条侧棱的截面都是平行四边形。
非正四棱柱3)过四棱柱不相邻的两条侧棱的截面都是平行四边形。
4)直四棱柱的侧棱长与高相等;直四棱柱的侧面及经过不相邻的两条侧棱的截面都是矩形。
特殊的四棱柱
正四棱柱是上、下底面都是正方形的直四棱柱。正四棱柱都是长方体,但长方体不都是正四棱柱。
侧棱等于底面边长(即六个面都是正方形)的正四棱柱是正方体。
正四角柱代表底面为正方形的四角柱,其对偶为正双四角锥。若侧面不是正方形也称为长方体,因为可以使用其中一个侧面当作底面。侧面也是正方形的正四角柱是正立方体,其具有正八面体对称性,对应的考克斯特群是BC3对称性,由于底面和侧面全等,因此每个顶点都是三个正方形(一个底面正方形和两个侧面正方形)的公共顶点,施莱夫利符号{4,3},其顶点图为正三角形,顶点布局为3(三个正方形,一个底面和两个侧面),在考克斯特-迪肯符号中以表示,由于侧面是正方形的正四角柱是正多面体,因此其对偶多面体也会是正多面体,即正八面体,也就是一个所有面都全等的正双四角锥。
体积与表面积
底面为任意四边形的四角柱的体积可以利用底面积乘以高来计算,若底面为凸四边形则可以透过底面的两个对角线向量与两个底面对角线交点向量的三阶行列式绝对值来计算:[4]
V凸四角柱=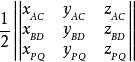
其中ABCD为底面四边形,AC、BD为凸四角柱底面四边形的两条对角线,对角线AC向量为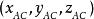 、对角线BD向量为
、对角线BD向量为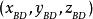 ,P为下底对角线交点、Q上底对角线交点,PQ为柱高,
,P为下底对角线交点、Q上底对角线交点,PQ为柱高,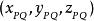 表示PQ向量
表示PQ向量
亦可写为向量积与数量积的形式:
V凸四角柱=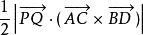
此种计算方法源自于底面积乘以高,而任意凸四角柱的底面一定是凸四边形,因此会适用于任意凸四边形的面积公式,可由对角线长与对角线夹角计算
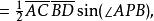 A底面积
A底面积
而此公式就直接对应到底面对角线向量的外积:
![]()
其中n为单位向量,但由于最后结果取绝对值所以被省略。
因此其表面积也可以利用此法计算,为底面积的两倍加上周长乘高:
A凸四角柱=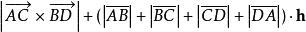



 求购
求购







