正七边形

在平面几何学中，正七边形是一个由七条相同长度的边和七个相同大小的角构成的 多边形。 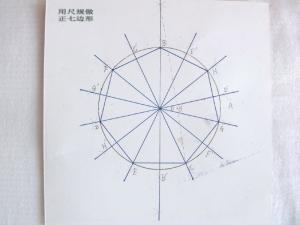正七边形

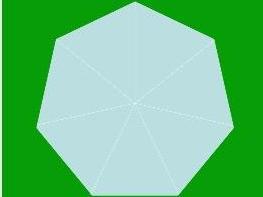正七边形  在一个正七边形里，每一个角的大小都是5π/7 rad，大约等于128.571 度。

正多边形的近似 面积公式

S正七边形≈3.634a^2

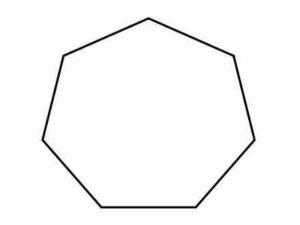正七边形  正七边形不能够单用没有刻度的 直尺和圆规来作图，不过若有一把有刻度的尺则可以。这种绘画的方法称之为纽西斯作图法。单用无刻度直尺和圆规不可能作出正七边形是因为，通过观察发现，2cos(2π/7) ≈ 1.247是最简 三次函数 x+ x- 2 x- 1的一个根。因此这个多项式是2cos(2π/7)的 最小多项式，同时这个最小多项式的多项式的次数（ 最高次幂）必须是2，属于可构造数。

近似正七边形的作法：

1，以圆心O，定长R为半径画圆，并作出两条互相垂直的直径MN，AP。

2，七等分直径MN。

3，以M为圆心，MN为半径画弧，交OA延长线于A1，交OP延长线于P1。

4，将A1，P1与直径上第2，4，6个等分点并延长，交圆周于B，C，D，E，F，G。

5，连接MBCDEFG则得正七边形。

这是一个近似的做法。

改进：由4步确定边长改为3 步确定边长

1；作圆，圆心为O

2；作 弦长为半径大小的弦AB

3；作弦AB的中垂线， 垂足为C

4；以OC为长度单位（OC即是所作正七边形边长），划分圆，并连接各分点，即是所求正七边形。

七边形的英文名称是heptagon，而有时也叫做septagon，"sept-"（septua-的元音 音节省略）是一个从 拉丁语引进的数学前缀）来表示“七、七的”，而不是hepta-（一个从 希腊语引进的数学前缀，应用于大多数英语中数学、化学等学术类术语命名的 前缀）。