离散小波变换

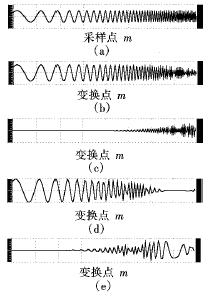离散小波变换获取最新　　余弦变换是经典的谱分析工具，他考察的是整个时域过程的频域特征或整个频域过程的时域特征，因此对于平稳过程，他有很好的效果，但对于非平稳过程，他却有诸多不足。在JPEG中，离散余弦变换将图像压缩为8×8 的小块，然后依次放入文件中，这种算法靠丢弃频率信息实现压缩，因而图像的压缩率越高，频率信息被丢弃的越多。在极端情况下，JPEG图像只保留了反映图像外貌的基本信息，精细的图像细节都损失了。小波变换是现代谱分析工具，他既能考察局部时域过程的频域特征，又能考察局部频域过程的时域特征，因此即使对于非平稳过程，处理起来也得心应手。他能将图像变换为一系列小波系数，这些系数可以被高效压缩和存储，此外，小波的粗略边缘可以更好地表现图像，因为他消除了DCT压缩普遍具有的方块效应。

在讨论复杂度之前，先做一些定义，当x[n]*y[n]时，x[n]之长度为N，y[n]之长度为L：

其中，

为(N+L-1)点离散傅里叶反转换(inverse discrete Fourier transform)

为(N+L-1)点离散傅里叶转换(discrete Fourier transform)

(1)一维离散小波变换之复杂度(没有分段卷积(sectioned convolution))：

(2)当 N >>> L 时，使用 “分段卷积(sectioned convolution)”的技巧：

将x[n]切成很多段，每段长度为，总共会有段，其中N_1>>L" src="https://upload.wikimedia.org/math/d/e/9/de97f120c146bb1b5bc739866f82591c.png">。

在这里要注意的是，当N>>L时，一维离散小波变换之复杂度是呈线性的(随N)

(3)多层(Multiple stages )的情况下

(4)二维离散小波变换之复杂度(没有分段卷积(sectioned convolution))：

上式中，第一部分需要M个一维离散小波变换并且每个一维离散小波变换的输入有N个点；第二部分需要N+L-1个一维离散小波变换并且每个一维离散小波变换的输入有M个点。

(5)二维离散小波变换之复杂度，使用 “分段卷积(sectioned convolution)”的技巧：

假设原始尺寸为，则每一小部分的尺寸为

所以若是使用分段卷积，则二维离散小波变换之复杂度是呈线性的(随MN)，。

(6)多层(Multiple stages )与二维的情况下：

首先x[m,n]的尺寸为，

1.若不细分，只细分时，总复杂度

2.若也细时分，总复杂度