- 共轭复数

共轭复数
基础定义
共轭复数,两个实部相等,虚部互为相反数的复数互为共轭复数(conjugate complex number)。当虚部不为零时,共轭复数就是实部相等,虚部相反,如果虚部为零,其共轭复数就是自身(当虚部不等于0时也叫共轭虚数)。复数z的共轭复数记作z(上加一横),有时也可表示为Z*。同时, 复数z(上加一横)称为复数z的复共轭(complex conjugate)。
公式
根据定义,若z=a+bi(a,b∈R),则![]() =a-bi(a,b∈R)。共轭复数所对应的点关于实轴对称(详见附图)。两个复数:x+yi与x-yi称为共轭复数,它们的实部相等,虚部互为相反数。在复平面上,表示两个共轭复数的点关于X轴对称,而这一点正是"共轭"一词的来源。两头牛平行地拉一部犁,它们的肩膀上要共架一个横梁,这横梁就叫做"轭"。如果用z表示x+yi,那么在z字上面加个"一"就表示x-yi,或相反。
=a-bi(a,b∈R)。共轭复数所对应的点关于实轴对称(详见附图)。两个复数:x+yi与x-yi称为共轭复数,它们的实部相等,虚部互为相反数。在复平面上,表示两个共轭复数的点关于X轴对称,而这一点正是"共轭"一词的来源。两头牛平行地拉一部犁,它们的肩膀上要共架一个横梁,这横梁就叫做"轭"。如果用z表示x+yi,那么在z字上面加个"一"就表示x-yi,或相反。
共轭复数有些有趣的性质:
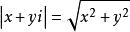 共轭复数
共轭复数
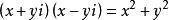 共轭复数
共轭复数
另外还有一些四则运算性质。
代数特征
(1)|z|=|![]() |;
|;
(2)z+![]() =2a(实数),z-
=2a(实数),z-![]() =2bi;
=2bi;
(3)z·![]() =|z|2=a2+b2(实数)。
=|z|2=a2+b2(实数)。
加法法则
复数的加法法则:设z1=a+bi,z2=c+di是任意两个复数。两者和的实部是原来两个复数实部的和,它的虚部是原来两个虚部的和。两个复数的和依然是复数。即 (a+bi)±(c+di)=(a±c)+(b±d)i.[2]
减法法则
两个复数的差为实数之差加上虚数之差(乘以i)
即:z1-z2=(a+ib)-(c+id)=(a-c)+(b-d)i
乘法法则
复数的乘法法则:把两个复数相乘,类似两个多项式相乘,结果中i2= -1,把实部与虚部分别合并。两个复数的积仍然是一个复数。
即:z1z2=(a+bi)(c+di)=ac+adi+bci+bdi2=(ac-bd)+(bc+ad)i.
除法法则
复数除法定义:满足(c+di)(x+yi)=(a+bi)的复数x+yi(x,y∈R)叫复数a+bi除以复数c+di的商运算方法:将分子和分母同时乘以分母的共轭复数,再用乘法法则运算。
即: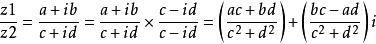 共轭复数
共轭复数
开方法则
若zn=r(cosθ+isinθ),则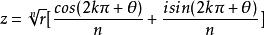 (k=0,1,2,3……n-1)
(k=0,1,2,3……n-1)
共轭法则
z=x+iy的共轭,标注为z*就是共轭数z*=x-iy
即:zz*=(x+iy)(x-iy)=x2-xyi+xyi-y2i2=x2+y2
即,当一个复数乘以他的共轭数,结果是实数。
z=x+iy 和 z*=x-iy 被称作共轭对。
运算特征
(1)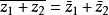
(2)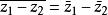
(3)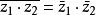
(4)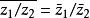 (z2≠0)
(z2≠0)
总结:和(差、积、商)的共轭等于共轭的和(差、积、商)。
应用举例
① | z1·z2| = |z1|·|z2|
②┃| z1|-| z2|┃≤| z1+z2|≤| z1|+| z2|
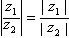 共轭复数③| z1-z2| = | z1z2|,是复平面的两点间距离公式,由此几何意义可以推出复平面上的直线、圆、双曲线、椭圆的方程以及抛物线
共轭复数③| z1-z2| = | z1z2|,是复平面的两点间距离公式,由此几何意义可以推出复平面上的直线、圆、双曲线、椭圆的方程以及抛物线
![]() 表示复数z的共轭复数,
表示复数z的共轭复数,![]() 表示复数z的共轭复数的共轭复数,即
表示复数z的共轭复数的共轭复数,即![]() =z。[3]
=z。[3]



 求购
求购







