泊松定理

[英] Poisson theorem

Poisson 分配

考虑下列现象：每小时服务台访客的人数，每天家中电话的通数，一本书中每页的错字数，某条道路上每月发生车祸的次数，生产线上的疵品数，学生到办公室找老师的次数……。大致上都有一些共同的特征：在某时间区段内，平均会发生若干次「事件」，但是有时候很少，有时又异常地多，因此事件发生的次数是一个随机变数，它所对应的机率函数称为 Poisson 分配。

在n重贝努力试验中，事件A在每次试验中发生的概率为p，出现A的总次数K服从二项分布b(n,p），当n很大p很小，λ=np大小适中时，二项分布可用参数为λ=np的泊松分布来近似。^[1]

一个 Poisson 过程有三个基本特性：

⑴在一个短时间区间内，发生一次事件的机率与成正比：。

⑵在短时间内发生两次以上的机率可以忽略。

⑶在不重叠的时间段落里，事件各自发生的次数是独立的。

另一名称为普阿松分布。关键应用n->；无穷大时二项分布(n,p）等价于参数为np的泊松分布验证　各位可以验证上述各种实际的例子，是不是相当符合 Poisson 过程的定义？

现令 P(k,T) 表示在时间区间 T 中发生 k 次事件的机率（注意 T 表示时间区间的长度，而不是绝对时间），由⑴⑵知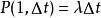，且，。现将 T 分割成 N 个短时间区段 （即），利用 ⑶各时间区段出现之事件是独立的条件，可知

（二项分配）

固定 k，当时

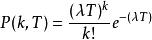（记得)

由上可知 Poisson 分配是二项分配 B(N,p,q) 的一种极限，其中 Np=常数，再让。另外，我们通常将记为 m，表示在时间区间 T 中，平均的发生次数（见下面习题）。

例题1

⑴验证。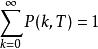

⑵令。求 E(X) 与 Var(X）。

（Ans. m,m.)

例1

.一公司之电话通数大约每小时 20 通，求在 5 分钟内一通电话也没有的机率？每小时 20 通，表示每分钟平均通/分。因此在 5 分钟的时间区间中，平均的电话通数为。所以

所以没有一通电话的机率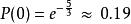。有了 P(k），我们可以回答许多类似的问题：在 5 分钟内有 4 通电话的机率是，大概每十六次才有一次。在 5 分钟内有超过 3 通电话的机率是

经计算这个机率分配的期望值，标准差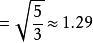。右图是 P(k) 的图形，当然由于 k= 0,1,…，所以这只是部分图形。读者可与一般的二项分配的图形比较。

例. 下表是 1910 年 Rutherford 观察放射性物质放射 α 粒子的记录，每次观察 7.5秒，共观察 2608 次。

粒子数次数频率P(k)

0 57 0.022 0.021

1 203 0.078 0.081

2 383 0.147 0.156

3 525 0.201 0.201

4 532 0.204 0.195

5 408 0.156 0.151

6 273 0.105 0.097

7 139 0.053 0.054

8 45 0.017 0.026

9 27 0.010 0.011

≥10 16 0.006 0.007

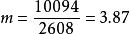
这里 P(k)=P(k,7.5），其中，m=3.87（见表最末栏），为 7.5 秒中 α粒子放射之平均个数。可以看到，如果假设 α 粒子的放射是一 Poisson 过程，结果相当吻合。

例2

. 令一放射性物质在时间 t 时所含之放射性粒子总量为 N(t），如果假设放射粒子是一 Poisson 过程，则在短时间 Δt后，

注意到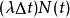是一期望值的形式。所以

这可看成辐射定律的「证明」。

对外搜寻关键字：

．辐射定律

指数分配与排队理论

令 W 表示在 Poisson 过程中，由开始到第一次事件发生的时间（这是一随机变数）。由上节知

P(W>t）=P（在[0,t]中无事件发生）

=

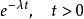
但

所以

这个机率分配称为指数分配。可计算得，这就是第一次事件发生的平均时间。另外，。

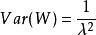让我们讨论排队理论。排队的现象无所不在：买各种票、吃自助餐、超商、百货公司……等。顾客揣度「应该排那一服务柜台会比较快？」「到底还要排多久？」是城市生活的基本问题；相对的，商家也要盘算到底在何时要开几个窗口柜台才符合成本，探讨这个问题的数学理论通称为排队理论，而指数分配经常被用到排队理论，当作服务客人时间（这是一随机变数）的机率密度函数。

让我们假设某柜台，服务客人的平均时间为 μ，想像在服务结束后，柜员会亮灯请下一位客人进来，则亮灯的平均时间是 μ。若将「灯亮」视为一事件发生，则亮灯的过程近似于一 Poisson 过程。而且前面定义的 W 正好表示两次亮灯间的间隔。所以 W 的机率密度函数是指数分配：

例3.

现假设一柜台平均服务时间为 3 分钟，设等待时间的机率密度函数为

⑴等候时间超过6分钟的机率是多少？

事实上，等候超过 T 分钟的机率是。

⑵另一个合理的问题是，如果在我前面还有另一个客人，则我怎么描述，我等待时间的机率分配呢？

令 W1是第一个客人等待的时间，W2是第一个客人开始被服务后，我所等待的时间，则 W1~ W2~ W3，而且总等待时间 U = W1+W2，另外显然 W1与 W2是互相独立的。所以我们的问题就是要计算 fU（t），由309页例子的方法，可以计算得

或者，如果将指数分配 fW(t) 想成是分配，则此相当于

因此如果我们想知道总等候时间不超过 5 分钟的机率，则

有一半的机会。

⑶如果前面有 n-1 个客人时，则可定义 U=W1+W2+ ···+ Wn，其中 Wi彼此独立，由 Gamma 分配性质知，即

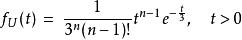
这告诉我们分配与排队理论的关系。我们将细节留作习题。

例题2

⑴超级市场一服务员平均服务时间为 2 分钟，若用指数分配当作等候时间之机率分配，则机率密度函数是什麼？

⑵如果他正开始服务一位客人，而你前面还有一位客人在等候，则你会等超过 6分钟的机率是多少？

⑶若服务员甲平均服务时间为 2 分钟，而服务员乙之平均服务时间为 3 分钟，如果你选择乙，你朋友选择甲，且一起开始接受服务，则你会比朋友快的机率是多少？（当然甲与乙的服务是相互独立的）你能给出一个一般的计算公式吗？