垂径定理

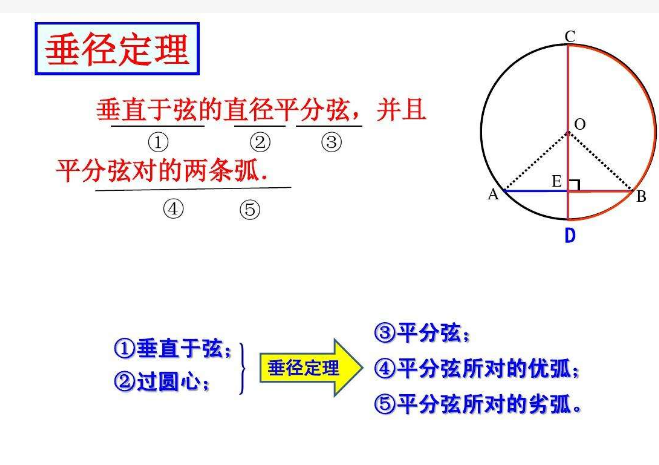垂径定理(3)垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

一条直线，在下列5条中只要具备其中任意两条作为条件,就可以推出其他三条结论。称为知二得三（知二推三）。

1. 平分弦所对的优弧
2. 平分弦所对的劣弧（前两条合起来就是：平分弦所对的两条弧）
3. 平分弦（不是直径）
4. 垂直于弦
5. 过圆心（或直径）

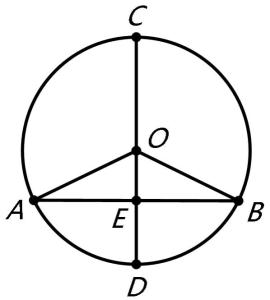垂径定理图示如图 ，在⊙O中，DC为直径， AB是弦，AB⊥DC于点E，AB、CD交于E，求证：AE=BE，弧AC=弧BC，弧AD= 弧BD

证明：连接OA、OB分别交⊙O于点A、点B

∵OA、OB是⊙O的半径

∴OA=OB

∴△OAB是等腰三角形

∵AB⊥DC

∴AE=BE，∠AOE=∠BOE（等腰三角形三线合一）

∴弧AD=弧BD，∠AOC=∠BOC

∴弧AC=弧BC

原本命题，其中CD垂直于直线AB推论一：平分弦（非直径）的直径垂直于这条弦,并且平分这条弦所对的两段弧。

几何语言：∵DC是直径，AE=EB

∴直径DC垂直于弦AB，劣弧AD=劣弧BD，弧AC=弧BC

推论二：平分弦所对的一条弧的直径垂直平分这条弦,并且平分这条弦所对的另一条弧。

几何语言：∵AE=BE，弧AD=弧BD

∴CD垂直平分AB，弧AC=弧BC

推论三：在同圆或者等圆中,两条平分弦所夹的弧相等。

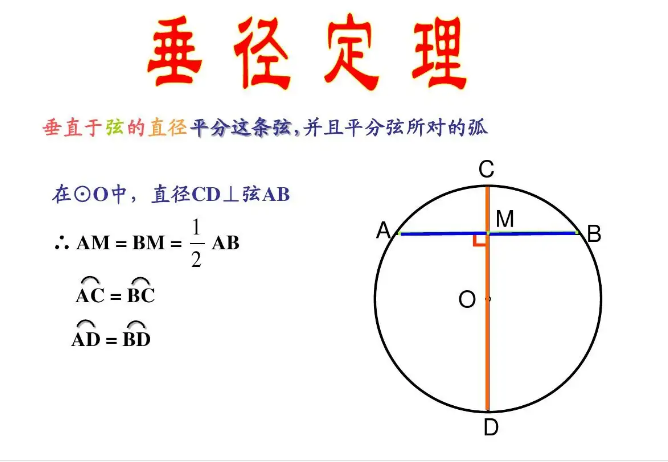垂径定理(3)欧几里得（古希腊数学家 希腊文：Ευκλειδης. ，公元前330年~公元前275年，）几何原本第I卷中的第12个命题实际即为垂径定理，这可能是最早的有关于垂径定理的记载。

垂径定理是圆的重要性质之一，它是证明圆内线段、角相等、垂直关系的重要依据，也为圆中的计算、证明和作图提供了依据、思路和方法。