重心定理

重心定理三角形的三条中线交于一点，这点到顶点的距离

是它到对边中点距离的2倍。该点叫做三角形的 重心。

三角形的重心是各中线的交点， 重心定理是说三角形顶点到重心的距离等于该顶点对边上中线长的2/3。

假设有n个物体组成的物体系，重量为wi,位于ri（矢量，下同）,i=1,2,...n. 则这个物体系的重心为r:

r=(w1r1+w2r2+...wnrn)/(w1+w2+...+wn)

这就是最一般的重心计算公式

物理学中可以使用微积分求出中心所在坐标。

如果知道A（x1，y1,z1),B(x2,y2,z2),C(x3,y3，z3）。则其 重心的坐标就为{(x1+x2+x3)/3,(y1+y2+y3)/3,(z1+z2+z3)/3}

利用三角形的相似性可以很快得到证明。

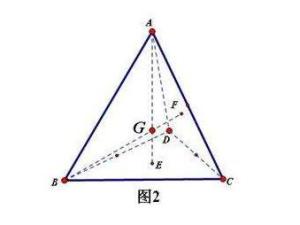
△ABC，AB、BC、CA中点分别为D、E、F，交于一点G。

∴DF//BC，DF=BC/2 ①（中位线定理）。

∴△ADF∽△ABC, E为BC中点，∴H为DF中点（可证AH/AE=DH/BE=HF/EC, BE=EC, ∴DH=HF)

∴HF=DF/2 , BE=BC/2， 又可由①知HF=BE/2

∴HF//BE.

又∵∠BGE=∠FGH。

∴△BGE∽△FGH

∴BG/GF=BE/HF=2。

∴BG=（2/3）BF

同样，利用公边定理及三角形的等高可轻易求得三条中线分得的六个三角形面积相等，通过面积亦可证明。