- 正交变换群

正交变换群
基本介绍
欧氏平面内的所有正交变换的集合构成群[2]。
证明:
(1)封闭性:设![]() 是两个正交变换,它们的系数方阵分别为
是两个正交变换,它们的系数方阵分别为![]() ,则
,则![]() 的系数方阵为
的系数方阵为
![]()
根据方阵的乘法法则,我们有:
![]() 但
但
![]() 所以
所以
![]() 因此
因此![]() 仍是正交变换。
仍是正交变换。
(2)逆元素:设A是正交变换T的方阵,且B是它的逆变换的方阵,则有:
![]() 因为
因为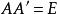 , 所以
, 所以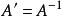 ,故
,故![]() , 所以
, 所以
![]() 因此其逆变换仍是正交变换。
因此其逆变换仍是正交变换。
由(1)(2)可得正交变换构成群[2]。
正交变换群的几何—欧氏几何
正交变换就是运动,可以说所谓欧氏几何就是正交变换群下的几何。即,研究在正交变换之下有那些不变的性质和不变的量。由正交变换的定义,“距离”是基本的不变量,由此可以推出一系列其他的不变性脚不变量。 · ·正交变换把任意图形F变成与它合同的图形F‘,但正交变换是构成群的,因此图形的合同关系具有下列性质: ·
1)图形F与自身常合同(反身性),恒等变换保证了这一性质。
2)如果图形F合同于F‘,则图形F’也合同于F(对称性),逆变换保证了这一性质。
3)如果图形F1合同于图形F2,图形F2合同于图形F3,则图形F1合同于图形F3(传递性),变换积保证了这一性质。
因此,图形的合同关系是一个等价关系。按着这—关系可将平面、(空间)内的所有图形进行分类,凡是合同的图形都属于同一个等价类,其中所有的图形都具有共同的几何性质,它们是正交变换下的不变性质;反过来,正交变换下的不变性质,也正是同一等价类图形的共同性质。
正交变换的几何就是研究正交变换下各等价类的共同性质,也就是正交变换下图形的不变性质和不变量。例如结合关系、顺序关系、合同关系、度量关系、平行关系,而这些关系都是欧几里得公理系统的推论,具体地说,这些不变性质和不变量也就是属于,介于、相交、平行、垂直、合同、角、正多边形、相似形、圆和其它二次曲线,长度、面积等,以及把这平面几何的性质推广到空间的一些性质等等,它们都是欧氏几何所研究的几何性质和量。可见,正交变换群的几何学就是欧氏几何学[3]。
相关概念
正交变换的定义和简单性质
定义平面上(或空间中)保持两点间距离不变的变换,叫做正交变换[3]。
显然,运动是正交变换。
正交变换有下列性质:
(1)两个正交变换的乘积是正交变换,正交变换的逆变换还是正交变换,这些都不难用正交变换的定义验证,容易看出正交变换的全体构成一个群,叫做正交变换群。
(2)正交变换把直线变成直线,为此,我们只需要证明,正交变换把共线的三点变成共线的三点.设P、Q、R是平面上顺序的三点,那么,它们在同一直线上的充要条件是:|PQ|+|QR|=|PR|。因为正交变换保持距离不变,所以变换之后,这个等式仍然成立,因此还在一条直线上。
利用上面的事实可以证明,空间中的正交变换还把平面变成平面。
(3)正交变换把相交直线(或平面)变成相交直线(或平面),平行直线(或平面)变成平行直线(或平面)。
平行直线(或平面)没有公共点,它们经过正交变换之后,根据变换是一一的和性质(2),仍然变成没有公共点的直线(或平面),即仍旧是平行直线(或平面)[3]。
(4)正交变换保持线段的分比不变。
由正交变换保持距离不变这一事实即可推出。
由性质(4)和(2),正交变换把线段变成线段,因为线段上的任意点把线段分成定比A,经过正交变换,A保持不变,所以线段上的点仍变成线段上的点,由此推出线段变成线段。
(5)正交变换保持角度不变。
实际上,设∠AOB(A、B是在角两边上任取的点)在正交变换下变成∠A'O'B'。因为正交变换保持距离不变,所以△AOB与△A'O'B'的对应边相等,于是
![]() 因此∠AOB=∠A'O'B'。
因此∠AOB=∠A'O'B'。
(6)正交变换把直角坐标系变成直角坐标系,而且任意点M的象M'在新坐标系里的坐标与点M在原坐标系里的坐标相同[3]。
因为正交变换即保持距离又保持角度不变,因此它把直角坐标系变为直角坐标系(图1)。
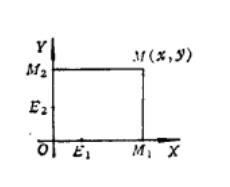 图1
图1
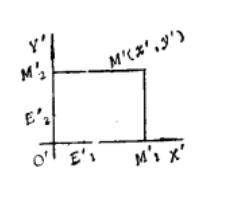 图2
图2
设点M的坐标为(x,y),因为正交变换保持分比不变,因而有
![]()
![]()
这表明M'在变换后的坐标系中的坐标与M在原坐标系中的坐标相同。其中,E1、E2分别是X轴与Y轴上的单位点;M1、M2分别是M在X轴与Y轴上的正投影。
对于空间的正交变换,也有同样的结果[3]。



 求购
求购




