共轭虚根

共轭虚根（conjugate imaginaryroots）又称共轭复根（conjugate complex roots），是一类特殊的共轭根。若非实复数a是实系数n次方程f(x)=0的根，则其共轭复数也是方程f(x)=0的根，且它们的重数相等，称α与为该方程的一对共轭虚根。^[1]

例1 求方程x²+1=0的根。

解：容易解出i和-i是该方程的一对共轭复（虚）根，且重数均为1。

1.实系数二次多项式

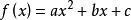的判别式为

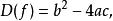当D(f)>0时，f(x)有两个相异实根；当D(f)=0时，f(x)有两个相等实根；D(f)<0时，f(x)有一对共轭虚根。^[1]

2.实系数三次多项式

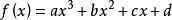的判别式为

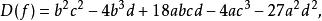当D(f)>0时，f(x)有三个相异实根；当D(f)=0时，f(x)有三个实根且至少有两个根相等；D(f)<0时，f(x)有一个实根和一对共轭虚根。^[1]