- 切向量

切向量
知识储备
在定义切向量之前,首先给出光滑函数的定义。叙述中都将按国际非线性学术界表达惯例,向量将一律用白斜体字母表示[2]。
定义1设A是![]() 的一个开子集(即A内每点都可找到一个完全属于A的邻域),
的一个开子集(即A内每点都可找到一个完全属于A的邻域),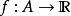 是一个函数。f点z
是一个函数。f点z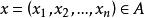 的值记为
的值记为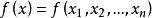 。如果f对
。如果f对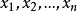 的任意阶偏导数存在且连续,则称函数f是
的任意阶偏导数存在且连续,则称函数f是![]() 类函数(function of class
类函数(function of class![]() ),简称f是一个
),简称f是一个![]() 函数或称f是一个光滑函数(smooth function)。如果函数f是
函数或称f是一个光滑函数(smooth function)。如果函数f是![]() 的,且对任意指定点
的,且对任意指定点![]() ,存在
,存在![]() 的一个邻域U,使对所有
的一个邻域U,使对所有![]() ,f在
,f在![]() 的Taylor级数展开式都收敛到
的Taylor级数展开式都收敛到![]() ,则称f是一个
,则称f是一个![]() 函数或称f 是一个解析函数( analytic function)。
函数或称f 是一个解析函数( analytic function)。
定义2一流形N上有定义的所有光滑函数的集合,记为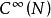 。在流形N上一点p的邻域有定义的所有光滑函数的集合,记为
。在流形N上一点p的邻域有定义的所有光滑函数的集合,记为![]() 。[2]
。[2]
定义
设N是一个n维光滑子流形,![]() 是在N上p点有定义的光滑函数集合,
是在N上p点有定义的光滑函数集合,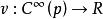 是定义在
是定义在![]() 上的泛函(算子),如果v有下列性质(也称求导性质)[2]:
上的泛函(算子),如果v有下列性质(也称求导性质)[2]:
(1)线性性
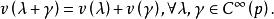
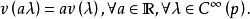
(2)符合Leibnitz规则[2]
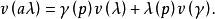
则称v是定义在流形N上某点p的一个切向量(tangent vector)。
相关概念介绍
下面对以上定义作一些概念性说明[2]。
(1)流形(manifold)是拓扑学和微分几何中的重要概念。不过,为不涉及过多的数学基础,此处不准备作严格的定义。从概念上说,一个n维流形可理解为由多个同为n维的曲面(或超曲面)经拼接所得到的曲面(或超曲面)。
(2)流形的一个特征是,它的一个局域可以与一个n维欧氏空间之间建立起点与点间的一对一映射关系,它的每个局域可以分别与各自的一个n维欧氏空间之间建立起点与点间的一对一映射关系,并可在此基础上建立起通用于各局域的流形局部坐标系,从而变成可度量的( metrizable)。
(3)具有微分结构的流形被称为微分流形(differential manifold)。这里所说的微分结构,是指参与拼接的曲面(或超曲面)彼此拼接得是如此之好,以至于流形作为一整体与n维欧氏空间之间的映射能达到任意次可微的程度,即达到光滑的程度。因此微分流形也称为光滑流形(smooth manifold)或简称流形。微分流形可理解为是由多个同为n维的光滑曲面(或超曲面)经拼接所得到的光滑曲面(或超曲面),也就是有任意阶导数的n维曲面(或超曲面)。
(4)定义在流形N上的光滑函数![]() 就是定义在流形N的局部坐标系上的函数。对于一个光滑流形而言,其各阶导数都存在。
就是定义在流形N的局部坐标系上的函数。对于一个光滑流形而言,其各阶导数都存在。
(5)光滑函数![]() 在某方向上的变化率,一般称为方向导数(directional derivative)。方向导数取值是一实数。算子v表示求方向导数的操作,故其映射关系可表示为
在某方向上的变化率,一般称为方向导数(directional derivative)。方向导数取值是一实数。算子v表示求方向导数的操作,故其映射关系可表示为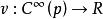 。
。
(6)求导的方向在函数![]() 的定义域上表示,即指的是流形局部坐标平面(或超平面)上定的方向,而不是指在
的定义域上表示,即指的是流形局部坐标平面(或超平面)上定的方向,而不是指在![]() 曲面的切平面(或超切平面)上定的方向。
曲面的切平面(或超切平面)上定的方向。
切向量和方向导数有密切关系,但这是两个不同的概念。切向量被定义为一个抽象的泛函(算子),指的是![]() 至欧氏空间
至欧氏空间![]() 的一个映射,而方向导数则指的是该映射的像值[2]。
的一个映射,而方向导数则指的是该映射的像值[2]。
例题解析
(流形![]() 上的切向量,切向量和方向导数的差异)设
上的切向量,切向量和方向导数的差异)设![]() 是定义在
是定义在![]() 上的
上的![]() (光滑)函数
(光滑)函数![]() 在点x的方向导数(即
在点x的方向导数(即![]() 在定义域一定方向上的坡度或变化率)定义为[2]
在定义域一定方向上的坡度或变化率)定义为[2]
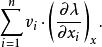
式中,![]() 是表示方向的系数。方向可以是给定的方向,也可以是某个体现函数
是表示方向的系数。方向可以是给定的方向,也可以是某个体现函数![]() 自身性质的方向。
自身性质的方向。
比如,![]() 在点x的梯度(gradient)被定义为向量
在点x的梯度(gradient)被定义为向量
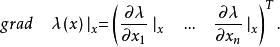
![]() 在点x的方向导数在此方向有最大坡度值
在点x的方向导数在此方向有最大坡度值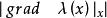 ,梯度方向是
,梯度方向是![]() 上升最陡的方向,所体现的就是函数
上升最陡的方向,所体现的就是函数![]() 自身的性质。
自身的性质。
如果把式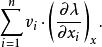 改写成
改写成
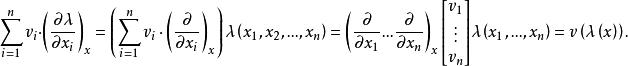
注:其中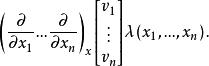 中的三部分分别为切向量的基底、方向向量、光滑函数,这三部分组成一个切向量;
中的三部分分别为切向量的基底、方向向量、光滑函数,这三部分组成一个切向量;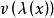 为方向导数。
为方向导数。
可见方向导数可拆成三部分。方向导数的前面两部分,即切向量的基底和方向向量合称为切向量。此切向量完全符合切向量定义。
方向的表示方法一般有两种。一种是用方向余弦向量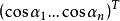 表示,另一种是用方向数向量
表示,另一种是用方向数向量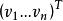 表示。切向量的方向一般都用后一种表示。方向数向量归一化后等于方向余弦向量。也可以说方向数向量等于方向余弦向量外乘一个常数。该常数表示向量的长度或大小。所以通常所说的方向向量不仅指方向,还可能包括其长度。切向量的方向和大小都是点的函数。在不同点上,不仅方向可能不同,而且外乘的常数(向量的长度)也可能会随之不同。尽管方向数向量有外乘常数,不仅表示方向,但为方便,以后仍将把它们和方向余弦向量一样看待,一律笼统地称为方向向量。[2]
表示。切向量的方向一般都用后一种表示。方向数向量归一化后等于方向余弦向量。也可以说方向数向量等于方向余弦向量外乘一个常数。该常数表示向量的长度或大小。所以通常所说的方向向量不仅指方向,还可能包括其长度。切向量的方向和大小都是点的函数。在不同点上,不仅方向可能不同,而且外乘的常数(向量的长度)也可能会随之不同。尽管方向数向量有外乘常数,不仅表示方向,但为方便,以后仍将把它们和方向余弦向量一样看待,一律笼统地称为方向向量。[2]



 求购
求购







