- 切线长
切线长
定义
切线长
路线交点至曲线起点或终点的直线距离。
圆的切线长
在经过圆外一点的切线，这一点和切点之间的线段叫做这点到圆的切线长。
解释：在图3中PA和PB所在直线就是两条切线，而线段PA与线段PB就叫切线长。
切线长定理
概述
从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线，平分两条切线的夹角。
推论
圆的外切四边形的两组对边的和相等。
推广
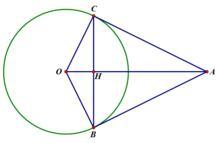连接BC，则BC⊥AO （如右图）
证明：连接BC。设BC与AO交于H
∵BO、CO是半径
∴BO=CO
∵∠ABO=∠ACO=90°
BO=CO
AO=AO
∴RtΔABO≌RtΔACO（HL）
∴∠AOC=∠AOB
∵CO=BO
∠AOC=∠AOB
OH=OH
∴△COH≌△BOH
∴∠CHO=∠BHO
∵∠CHO+∠BHO=180°
∴∠CHO=∠BHO=90°
∴BC⊥AO
定理
从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。
切线长公式
过圆X²+Y²+DX+EY+F=0外一点M（a，b）引切线，切点为T，则IMTI的平方=a²+b²+Da+Eb+F.
相关百科
求购