- 收敛数列
收敛数列
性质
唯一性
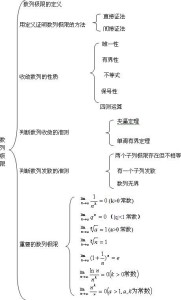思维导图如果数列Xn收敛，每个收敛的数列只有一个极限。
有界性
定义：设有数列Xn , 若存在M>0,使得一切自然数n,恒有|Xn|<M成立，则称数列Xn有界。
定理1：如果数列{Xn}收敛，那么该数列必定有界。推论：无界数列必定发散；数列有界
，不一定收敛；数列发散不一定无界。
数列有界是数列收敛的必要条件，但不是充分条件
保号性
如果数列{Xn}收敛于a，且a>0（或a<0），那么存在正整数N，当n>N时，都有Xn>0（或Xn<0）。
相互关系
收敛数列(3)收敛数列与其子数列间的关系
子数列也是收敛数列且极限为a恒有|Xn|<M
若已知一个子数列发散，或有两个子数列收敛于不同的极限值，可断定原数列是发散的。
如果数列{
}收敛于a，那么它的任一子数列也收敛于a。
相关百科
求购