σ代数

在数学中，某个集合X上的σ代数又叫σ域、完全加法类、可列加法类、σ加法类，是含有基本空间的σ环，是X的所有子集的集合（也就是幂集）的一个子集。^[1]

这个子集满足对于可数个集合的并集运算和补集运算的封闭性（因此对于交集运算也是封闭的）。σ代数可以用来严格地定义所谓的“可测集”，是测度论的基础概念之一。需要注意的是，虽然σ代数也称做σ域，但是它是布尔代数。^[2]

设г是由集合X中一些子集所构成的集合族(也叫做集类^[3])，且满足下述条件：

（1）X∈г；

（2）若A∈г，则A的补集Ac∈г；

（3）若AN∈г（N=1,2,…）则∪AN∈г；

我们称г是一个σ代数。

我们首先定义集代数，然后通过集代数定义σ代数。

X为集合，P(X)为其幂集，ω是P(X)的子集，且满足

(1) X∈ω

(2) 如A∈ω，则A的补集∈ω

(3) 如A∈ω，B∈ω，则A∪B∈ω.

则称ω为X上的集代数。

ω是X上的集代数，如ω还满足：如果A_i∈ω，i=1,2,3,…,则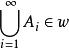，就称ω是X上的σ代数。^[2]

σ代数的概念大约起始于二十世纪的前三十年，它随着测度论的发展而逐渐清晰。最著名的σ代数是关于实数轴测度的波莱尔σ代数（得名于法国数学家埃米·波莱尔），以及1901年亨利·勒贝格建立的勒贝格σ代数。而现代的测度理论的公理化体系就建立在勒贝格的相关理论之上。在这个领域中，σ代数不仅仅是用于建立公理体系，也是一个强有力的工具，在定义许多重要的概念如条件期望和鞅的时候，都需要用到。