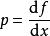- 勒让德变换

勒让德变换
概述
为了研究一个系统内部蕴藏的数学结构,表述此系统的函数关系改用一个新函数来表示,其变数是的导数,。而的值是如右图蓝线在 y 轴的负截距
换句话说,从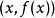 x 值到 y 值的函数,转换成
x 值到 y 值的函数,转换成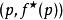 f(x) 在 x 点的导数到在 x 点切线 y 截距的函数
f(x) 在 x 点的导数到在 x 点切线 y 截距的函数
这程序是由阿德里安-马里·勒壤得所发明的,因此称为勒让德变换。称函数![]() 为
为![]() 的勒让德变换;
的勒让德变换;
用方程表示
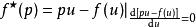 。
。
此式子表示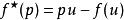 中的 u 对
中的 u 对![]() 而言是个参数,且参数 u 会满足
而言是个参数,且参数 u 会满足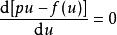 的
的![]() 。即求算表达式关于变数
。即求算表达式关于变数![]() 的极值。
的极值。
为方便讨论,把讨论限定在![]() 为严格单调递增。会有这方程是因为在
为严格单调递增。会有这方程是因为在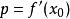 也就是斜率不变的状况下,对每个
也就是斜率不变的状况下,对每个![]() 而言,所有与曲线
而言,所有与曲线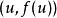 相交且斜率为
相交且斜率为![]() 的直线族为
的直线族为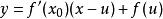 。若令
。若令![]() ,该直线即是
,该直线即是![]() 在
在![]() 的切线方程。把x当作常数并由右图直接观察可知,在
的切线方程。把x当作常数并由右图直接观察可知,在![]() 的情况下,
的情况下,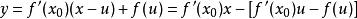 值是最小的,也就是说直线方程中
值是最小的,也就是说直线方程中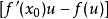 这部分是最大的,而正好
这部分是最大的,而正好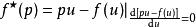 ,正是原方程所求的极值。
,正是原方程所求的极值。
勒让德变换是点与线之间对偶性关系(duality)的一个应用。函数![]() 设定的函数关系可以用
设定的函数关系可以用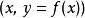 点集合来表示;也可以用切线(在严格单调递增的讨论下,切线跟导数p有一对一的关系)集合表示。
点集合来表示;也可以用切线(在严格单调递增的讨论下,切线跟导数p有一对一的关系)集合表示。
若将勒让德变换广义化,则会变为勒壤得-芬伽转换(Legendre-Fenchel transformation)。勒让德变换时常用于热力学与哈密顿力学。
定义
最大值式定义
更详细地定义勒让德变换,为了求得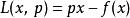 关于
关于![]() 的最大值,设定
的最大值,设定![]() 关于{\displaystyle x\,\!}的偏导数为零:
关于{\displaystyle x\,\!}的偏导数为零:
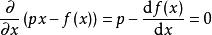 。
。
则
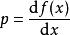 。(1)
。(1)
这表达式必为最大值。因为,凸函数![]() 的二阶导数是负数:
的二阶导数是负数:
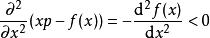 ;
;
用方程 (1) 来计算函数![]() 的反函数
的反函数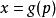 。代入
。代入![]() 方程,即可以得到想要的形式:
方程,即可以得到想要的形式:
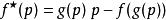 。
。
计算![]() 的勒让德变换,所需的步骤为:
的勒让德变换,所需的步骤为:
找出导函数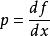 ,
,
计算导函数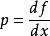 的反函数
的反函数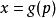 ,
,
代入![]() 方程来求得新函数
方程来求得新函数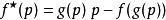 。
。
这定义切确地阐明:勒让德变换制造出一个新函数![]() ;其新自变数为
;其新自变数为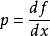 。
。
反函数式定义
另外一种勒让德变换的定义是:假若两个函数![]() 与
与![]() 的一阶导数是互相的反函数;
的一阶导数是互相的反函数;
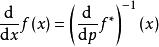 ,
,
或者,
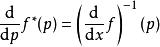 ,
,
则![]() 与
与![]() 互相为彼此的勒让德变换。
互相为彼此的勒让德变换。
依照定义,
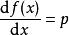 ,
,
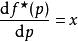 。
。
思考下述运算:
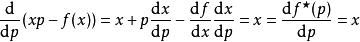 。
。
所以,
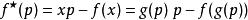 ;
;
这里, 。
。
这答案是标准答案;但并不是一个答案。设定
 ,
,
也可以满足定义的要求。在某些情况下(例如:热力势(thermodynamic potential),会采用非标准的答案。除非另外注明,此页面一律采用标准答案。
应用
热力学
![]()
![]()
![]() 在热力学里,使用勒让德变换主要的目的是,将一个函数与所含有的一个自变数,转换为一个新函数与所含有的一个新自变数,(此新自变数是旧函数对于旧自变数的偏导数);将旧函数减去新自变数与旧自变数的乘积,得到的差就是新函数。勒让德变换可以用来在各种热力势(thermodynamic potential)之间作转换。例如,内能是外延量(extensive)熵,体积,与化学成分(chemical composition)
在热力学里,使用勒让德变换主要的目的是,将一个函数与所含有的一个自变数,转换为一个新函数与所含有的一个新自变数,(此新自变数是旧函数对于旧自变数的偏导数);将旧函数减去新自变数与旧自变数的乘积,得到的差就是新函数。勒让德变换可以用来在各种热力势(thermodynamic potential)之间作转换。例如,内能是外延量(extensive)熵,体积,与化学成分(chemical composition)![]() 的显函数
的显函数
 。
。
对于![]() ,函数
,函数![]() (非标准的)勒让德变换为焓函数
(非标准的)勒让德变换为焓函数![]() :
:
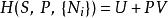 ,
,
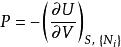 。
。
一个熵与内含量(intensive)压力的函数。当压力是常数时,这函数很有用。
对于![]() ,函数
,函数![]() 勒让德变换为吉布斯能函数
勒让德变换为吉布斯能函数![]() :
:
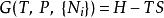 ,
,
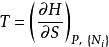 。
。
对于![]() ,函数
,函数![]() 勒让德变换为亥姆霍兹自由能函数
勒让德变换为亥姆霍兹自由能函数![]() :
:
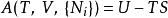 ,
,
 。
。
这些自由能函数时常用在常温的物理系统。
经典力学
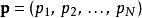
![]()
![]()
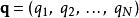
![]() 在经典力学里,勒让德变换专门用来从拉格朗日表述导引出哈密顿表述,或反导之。拉格朗日量是广义坐标与广义速度的函数;而哈密顿量将函数的自变量转换为广义坐标
在经典力学里,勒让德变换专门用来从拉格朗日表述导引出哈密顿表述,或反导之。拉格朗日量是广义坐标与广义速度的函数;而哈密顿量将函数的自变量转换为广义坐标![]() 与广义动量:
与广义动量:
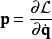 ,
,
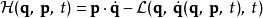 。
。
正则变换
正则变换广泛地应用勒让德变换在其理论里。正则变换是一种正则坐标的改变, ,而同时维持哈密顿方程的形式,虽然哈密顿量可能会改变。正则变换的方程为
,而同时维持哈密顿方程的形式,虽然哈密顿量可能会改变。正则变换的方程为
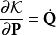 ,
,
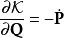 ,
,
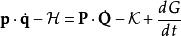 ;
;
这里,![]() 是旧正则坐标,
是旧正则坐标,![]() 是新正则坐标,
是新正则坐标,![]() 是旧哈密顿量,
是旧哈密顿量,![]() 是新哈密顿量,
是新哈密顿量,![]() 是生成函数。
是生成函数。



 求购
求购